题目内容

已知
a
=（1，2），
b
=（-2，1），
u
=
a
+2
b
，则与向量
μ
同向的单位向量
μ0
等于
 
．
考点：向量的加法及其几何意义,单位向量
专题：平面向量及应用
分析：先求出
u
的坐标表示，再求与向量
μ
同向的单位向量
μ0
=
u
|
u
|
即可．
解答： 解：∵
a
=（1，2），
b
=（-2，1），
∴
u
=
a
+2
b
=（1-2×2，2+2×2）=（-3，6），
∴与向量
μ
同向的单位向量为
μ0
=
u
|
u
|
=
(-3，6)
(-3)2+62
=（-
5
5
，
2
5
5
）．
故答案为：（-
5
5
，
2
5
5
）．
点评：本题考查了平面向量的应用问题，解题时应根据平面向量的坐标运算进行解答，是基础题．
练习册系列答案
相关题目
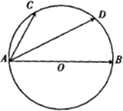
如图，AB是⊙O的直径，点C，D是半圆弧AB上的两个三等分点，
AB
=
a
，
AC
=
b
，则
AD
=（　　）
A、
1
2
a
+
b
B、
1
2
a
-
b
C、
a
+
1
2
b
D、
a
-
1
2
b
已知a＞0，b＞0且a+b=1．
求证：（1）
1
a
+
1
b
≥4；
（2）
a+
1
2
+
b+
1
2
≤2．
2
C
1
99
-4
C
2
99
+8
C
3
99
-16
C
4
99
+…+299
C
99
99
=
 
．
已知双曲线x2-
y2
2
=1的顶点、焦点分别为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点、顶点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）已知一直线l过椭圆C的右焦点F2，交椭圆于点A、B．当直线l与两坐标轴都不垂直时，在x轴上是否总存在一点P，使得直线PA、PB的倾斜角互为补角？若存在，求出P坐标；若不存在，请说明理由．
下列函数中，既是偶函数又在（-∞，0）上单调递增的是（　　）
A、y=x3
B、y=cosx
C、y=(
1
2
)|x|
D、y=x2
若f（x）=x2-2ax+4在（-∞，2]上是减函数，则a的取值范围是
 
．
函数f（x）是定义域在R上的奇函数．若x≥0时f（x）=x2+2x，则f（-2）等于（　　）
A、8B、4C、-8D、0
已知二次函数f（x）=x2+bx+c，且方程f（x）+4=0有唯一解x=1，
（1）求函数f（x）的解析式；
（2）若函数f（x）在区间[a，a+4]上存在零点，请写出实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网