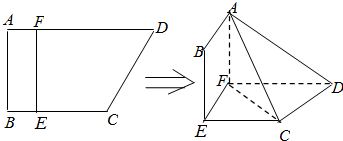
题目内容
设变量x、y满足约束条件
,则x2+y2的最大值为 .
|
考点:简单线性规划
专题:数形结合
分析:作出变量x、y满足约束条件所表示的可行域,然后根据x2+y2的几何意义,从而得到答案.
解答:
解:画出满足约束条件
的平面区域,
如图示:
 ,
,
∴x2+y2的最大值是C点到原点的距离的平方,
∴x2+y2=25,
故答案为:25.
|
如图示:
 ,
,∴x2+y2的最大值是C点到原点的距离的平方,
∴x2+y2=25,
故答案为:25.
点评:本题主要考查了利用线性规划求最值,属中等题.解题的关键是做出可行域然后利用目标函数的几何意义进行求解.

练习册系列答案
相关题目
原点和点(1,1)在直线x+y=a两侧,则a的取值范围是( )
| A、0<a<2 |
| B、a<0或a>2 |
| C、a=0或a=2 |
| D、0≤a≤2 |
如图,AB是⊙O的直径,点C,D是半圆弧AB上的两个三等分点,
=
,
=
,则
=( )
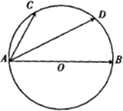
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
为了得到函数y=31-x的图象,可以把函数y=3-x的图象( )
| A、向左平移3个单位长度 |
| B、向右平移3个单位长度 |
| C、向左平移1个单位长度 |
| D、向右平移1个单位长度 |
下列函数中,既是偶函数又在(-∞,0)上单调递增的是( )
| A、y=x3 | ||
| B、y=cosx | ||
C、y=(
| ||
| D、y=x2 |