题目内容
已知函数f(x)=|1-
|(x>0),当0<a<b,若f(a)=f(b)时,则有( )
| 1 |
| x |
| A、ab>1 | ||
| B、ab≥1 | ||
C、ab≥
| ||
D、ab>
|
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:由题意可得f(x)=
,故f(x)在(0,1)内递减,在(1,+∞)内递增.由0<a<b,且f(a)=f(b),可得
+
=2,再利用基本不等式求得ab>1.
|
| 1 |
| a |
| 1 |
| b |
解答:
解:∵x>0,当x≥1时,1-
≥0,f(x)=|1-
|=1-
,
当x<1时,1-
<0,f(x)=|1-
|=
-1,
∴f(x)=
.
∴f(x)在(0,1)内递减,在(1,+∞)内递增.
由0<a<b,且f(a)=f(b)⇒0<a<1<b,
∴
-1=1-
,即
+
=2,∴2>2
,解得ab>1,
故选:A.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
当x<1时,1-
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
∴f(x)=
|
∴f(x)在(0,1)内递减,在(1,+∞)内递增.
由0<a<b,且f(a)=f(b)⇒0<a<1<b,
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
|
故选:A.
点评:本题考查的知识点是带绝对值的函数,基本不等式的应用,其中根据绝对值的定义去掉绝对值符号,将函数的解析式化为分段函数的形式是解答的关键,属于中档题.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
已知△ABC的周长为
+1,且sinA+sinB=
sinC.若△ABC的面积为
sinC,则角C的大小为( )
| 2 |
| 2 |
| 1 |
| 6 |
| A、30° | B、60° |
| C、90° | D、120° |
 一个正三棱柱的每一条棱长都是a,则经过底面一边和相对侧棱的一个端点的截面(即图中△ACD)的面积为( )
一个正三棱柱的每一条棱长都是a,则经过底面一边和相对侧棱的一个端点的截面(即图中△ACD)的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
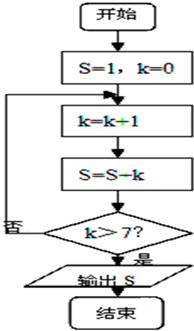 执行如图所示的程序框图,则输出的结果是( )
执行如图所示的程序框图,则输出的结果是( )| A、28 | B、29 | C、36 | D、37 |
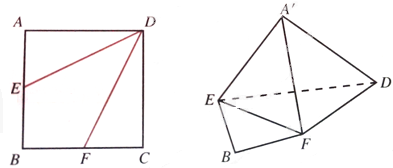

 在三棱柱ABC-A1B1C1中,侧面ABBA1为矩形,AB=1,AA1=
在三棱柱ABC-A1B1C1中,侧面ABBA1为矩形,AB=1,AA1=