题目内容
设函数f(x)=ax2+x-a,x∈[-1,1]的最大值为M(a),则当a∈[-1,1]时M(a)的最大值为 .
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:讨论a的取值,根据二次函数单调性和对称轴之间的关系即可得到结论.
解答:
解:若a=0,则f(x)=x,当x∈[-1,1]的最大值为M(a)=1.
若a≠0,二次函数的对称轴x=-
,
若0<a<1,则-
≤-
.此时当x=1时,函数取得最大值为M(a)=f(1)=a+1-a=1,
若=-1≤a<0,则-
≥
.此时当x=-1时,函数取得最大值为M(a)=f(-1)=a-1-a=-1,
综上M(a)的最大值为1,
故答案为:1
若a≠0,二次函数的对称轴x=-
| 1 |
| 2a |
若0<a<1,则-
| 1 |
| 2a |
| 1 |
| 2 |
若=-1≤a<0,则-
| 1 |
| 2a |
| 1 |
| 2 |
综上M(a)的最大值为1,
故答案为:1
点评:本题主要考查函数最值的计算,根据二次函数单调性和对称轴之间的关系是解决本题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知函数f(x)=|1-
|(x>0),当0<a<b,若f(a)=f(b)时,则有( )
| 1 |
| x |
| A、ab>1 | ||
| B、ab≥1 | ||
C、ab≥
| ||
D、ab>
|
长方体ABCD-A1B1C1D1,AB=2,AD=2,AA1=
,则点D到平面ACD1的距离是( )
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
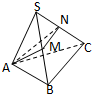 如图,三棱锥S-ABC中,SA=AB=AC=2,∠ASB=∠BSC=∠CSA=30°,M、N分别为SB、SC上的点,则△AMN周长最小值为
如图,三棱锥S-ABC中,SA=AB=AC=2,∠ASB=∠BSC=∠CSA=30°,M、N分别为SB、SC上的点,则△AMN周长最小值为