题目内容
已知圆心为C的圆过点A(0,-6)和B(1,-5),且圆心在直线l:x-y+1=0上.
(1)求圆心为C的圆的标准方程;
(2)过点M(2,8)作圆的切线,求切线方程.
(1)求圆心为C的圆的标准方程;
(2)过点M(2,8)作圆的切线,求切线方程.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)设圆的标准方程,用待定系数的方法,求得圆的方程;(2)点斜式设出直线方程,圆心到切线的距离等于半径,得到方程,注意斜率不存在的情况.
解答:
(本小题12分)
解:(1)设所求的圆的方程为(x-a)2+(y-b)2=r2
依题意得:
…(3分)
解得:a=-3,b=-2,r2=25
所以所求的圆的方程为:(x+3)2+(y+2)2=25…(6分)
(2)设所求的切线方程的斜率为k,则切线方程为y-8=k(x-2),即kx-y-2k+8=0
又圆心C(-3,-2)到切线的距离d=
=
又由d=r,即
=5,解得k=
…(8分)
∴所求的切线方程为3x-4y+26=0…(10分)
若直线的斜率不存在时,即x=2也满足要求.
∴综上所述,所求的切线方程为x=2或3x-4y+26=0…(12分)
解:(1)设所求的圆的方程为(x-a)2+(y-b)2=r2
依题意得:
|
解得:a=-3,b=-2,r2=25
所以所求的圆的方程为:(x+3)2+(y+2)2=25…(6分)
(2)设所求的切线方程的斜率为k,则切线方程为y-8=k(x-2),即kx-y-2k+8=0
又圆心C(-3,-2)到切线的距离d=
| |-3k+2-2k+8| | ||
|
| |5k-10| | ||
|
又由d=r,即
| |5k-10| | ||
|
| 3 |
| 4 |
∴所求的切线方程为3x-4y+26=0…(10分)
若直线的斜率不存在时,即x=2也满足要求.
∴综上所述,所求的切线方程为x=2或3x-4y+26=0…(12分)
点评:本题考查圆的方程及圆的切线的求法,注意掌握基本概念与方法.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
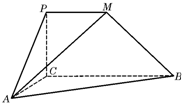 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.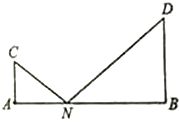 如图,C,D是两个小区的所在地,C,D到一条公路AB的垂直距离CA=1km,DB=2km,AB两端之间的距离为4km,某公交公司将在AB之间找一点N,在N处建造一个公交站台.
如图,C,D是两个小区的所在地,C,D到一条公路AB的垂直距离CA=1km,DB=2km,AB两端之间的距离为4km,某公交公司将在AB之间找一点N,在N处建造一个公交站台. 如图所示,等边△ABC的边长为2,以A为圆心,半径为1作圆,PQ是圆的直径,求
如图所示,等边△ABC的边长为2,以A为圆心,半径为1作圆,PQ是圆的直径,求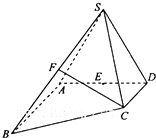 如图,在四棱锥S-ABCD中,己如AB∥DC,AB⊥AD,△SAD是正三角形,AD=AB=2DC=2,SC=
如图,在四棱锥S-ABCD中,己如AB∥DC,AB⊥AD,△SAD是正三角形,AD=AB=2DC=2,SC=