题目内容
12．设函数$f（x）=\left\{\begin{array}{l}{log_{\frac{1}{2}}}（x+1），0≤x≤1\\ f（x-1），x＞1\end{array}\right.$，则$f（\sqrt{2}）$的值是（ ）| A． | 2 | B． | -2 | C． | $\frac{1}{2}$ | D． | $-\frac{1}{2}$ |
分析 由已知中函数$f（x）=\left\{\begin{array}{l}{log_{\frac{1}{2}}}（x+1），0≤x≤1\\ f（x-1），x＞1\end{array}\right.$，将x=$\sqrt{2}$代入计算，可得答案．
解答 解：$f（{\sqrt{2}}）=f（{\sqrt{2}-1}）={log_{\frac{1}{2}}}（{\sqrt{2}-1+1}）=-\frac{1}{2}$，
故选D．
点评 本题考查的知识点是分段函数的应用，函数求值，难度中档．
练习册系列答案
一线名师权威作业本系列答案
相关题目
17．已知P（x0，y0）是抛物线y2=2px（p＞0）上的一点，过P点的切线方程的斜率可通过如下方式求得，在y2=2px两边同时对x求导，得2yy'=2p，则$y'=\frac{p}{y}$，所以过点P的切线的斜率$k=\frac{p}{y_0}$，试用上述方法求出双曲线${x^2}-\frac{y^2}{2}=1$在$P（{\sqrt{2}，\sqrt{2}}）$处的切线方程为（ ）
| A． | 2x-y=0 | B． | $2x-y-\sqrt{2}=0$ | C． | $2x-3y-\sqrt{2}=0$ | D． | $x-y-\sqrt{2}=0$ |
4．
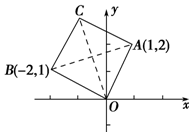如图在复平面上，一个正方形的三个顶点对应的复数分别是1+2i，-2+i，0，那么这个正方形的第四个顶点对应的复数为（ ）
如图在复平面上，一个正方形的三个顶点对应的复数分别是1+2i，-2+i，0，那么这个正方形的第四个顶点对应的复数为（ ）| A． | 3+i | B． | -1+3i | C． | 1-3i | D． | 3-i |
1．某几何体的三视图如图所示，其正视图，侧视图，俯视图均为全等的正方形，则该几何体的体积为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | $\sqrt{6}$ | D． | 2$\sqrt{6}$ |
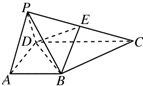已知在四棱锥P-ABCD中，底面ABCD是直角梯形，∠BAD=90°，2AB=2AD=CD，侧面PAD是正三角形且垂直于底面ABCD，E是PC的中点．