题目内容
17.已知P(x0,y0)是抛物线y2=2px(p>0)上的一点,过P点的切线方程的斜率可通过如下方式求得,在y2=2px两边同时对x求导,得2yy'=2p,则$y'=\frac{p}{y}$,所以过点P的切线的斜率$k=\frac{p}{y_0}$,试用上述方法求出双曲线${x^2}-\frac{y^2}{2}=1$在$P({\sqrt{2},\sqrt{2}})$处的切线方程为( )| A. | 2x-y=0 | B. | $2x-y-\sqrt{2}=0$ | C. | $2x-3y-\sqrt{2}=0$ | D. | $x-y-\sqrt{2}=0$ |
分析 把双曲线的解析式变形后,根据题中的例子,两边对x求导且解出y′,把P的坐标代入求出切线的斜率,然后根据切点P的坐标和求出的斜率,写出切线方程即可.
解答 解:由双曲线${x^2}-\frac{y^2}{2}=1$,得到y2=2x2-2,
根据题意,两边同时对x求导得:2yy′=4x,解得y′=$\frac{2x}{y}$,
由$P({\sqrt{2},\sqrt{2}})$,得到过P得切线的斜率k=2,
则所求的切线方程为:y-$\sqrt{2}$=2(x-$\sqrt{2}$),即2x-y-$\sqrt{2}$=0.
故选:B.
点评 此题考查了求导法则的运用,以及根据一点和斜率会写出直线的方程.本题的类型是新定义题,此类题的作法是认真观察题中的例题,利用类比的方法求出所求的切线方程.

练习册系列答案
相关题目
7.若α,β为锐角,tan(α+β)=3,$tanβ=\frac{1}{2}$,则α的值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
5.已知某三棱锥的三视图如图所示,正视图和俯视图都是等腰直角三角形,则该三棱锥中最长的棱长为( )

| A. | $2\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 2 |
12.设函数$f(x)=\left\{\begin{array}{l}{log_{\frac{1}{2}}}(x+1),0≤x≤1\\ f(x-1),x>1\end{array}\right.$,则$f(\sqrt{2})$的值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
2.在同一平面直角坐标系中,点A($\frac{1}{3}$,-2)经过伸缩变换φ:$\left\{\begin{array}{l}{x′=3x}\\{2y′=y}\end{array}\right.$所得的点A′的坐标为( )
| A. | (1,-1) | B. | (1,-4) | C. | $({\frac{1}{9},-4})$ | D. | (9,-1) |
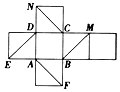 如图是正方体的平面展开图.关于这个正方体,有以下判断:①EC⊥平面AFN;
如图是正方体的平面展开图.关于这个正方体,有以下判断:①EC⊥平面AFN;