题目内容
数列{an}的前n项和为Sn，若
恒为非零常数k，则称数列{an}为“和谐数列”．
（1）公差不为零的等差数列{bn}的首项为1，且为“和谐数列”，求k的值及数列{bn}的通项公式；
（2）正项数列{xn}的前n项和为Tn，且2Tn=xn（xn+1），（n∈N*），判断数列{xn}是否为“和谐数列”，并说明理由．
| S 2n |
| S n |
（1）公差不为零的等差数列{bn}的首项为1，且为“和谐数列”，求k的值及数列{bn}的通项公式；
（2）正项数列{xn}的前n项和为Tn，且2Tn=xn（xn+1），（n∈N*），判断数列{xn}是否为“和谐数列”，并说明理由．
考点：数列的求和,数列的应用
专题：等差数列与等比数列
分析：（1）由已知条件推导出4dn+4-2d=kdn+2k-kd，解得
，由此能求出数列{bn}的通项公式．
（2）由2Tn=xn（xn+1），得2Tn=xn2+xn，由此能求出{xn}是以1为首项，以1为公差的等差数列，从而得到xn=n，数列{xn}不是“和谐数列”．
|
（2）由2Tn=xn（xn+1），得2Tn=xn2+xn，由此能求出{xn}是以1为首项，以1为公差的等差数列，从而得到xn=n，数列{xn}不是“和谐数列”．
解答：
解：（1）设{b1}的公差为d，则Sn=n+
d，S2n=
d，
由
=k，得
=k，
即
=k，
∴4dn+4-2d=kdn+2k-kd，
∴
，
又d≠0，∴
，
∴bn=1+（n-1）×2=2n-1．
（2）由2Tn=xn（xn+1），得2Tn=xn2+xn，①
当n=1时，2x1=x12+x1 ，又xn＞0，∴x1=1，
当n≥2时，2Tn-1=xn-12+xn-1，②
①-②，得：2xn=xn2+xn-xn-12-xn-1，
即（xn+xn-1）（xn-xn-1-1）=0，又xn＞0，
∴xn-xn-1=1，
∴{xn}是以1为首项，以1为公差的等差数列，
∴xn=n，
∵
=3≠
=
，
∴数列{xn}不是“和谐数列”．
| n(n-1) |
| 2 |
| 2n(2n-1) |
| 2 |
由
| S2n |
| Sn |
2n+
| ||
n+
|
即
| 4+2(2n-1)d |
| 2+(n-1)d |
∴4dn+4-2d=kdn+2k-kd，
∴
|
又d≠0，∴
|
∴bn=1+（n-1）×2=2n-1．
（2）由2Tn=xn（xn+1），得2Tn=xn2+xn，①
当n=1时，2x1=x12+x1 ，又xn＞0，∴x1=1，
当n≥2时，2Tn-1=xn-12+xn-1，②
①-②，得：2xn=xn2+xn-xn-12-xn-1，
即（xn+xn-1）（xn-xn-1-1）=0，又xn＞0，
∴xn-xn-1=1，
∴{xn}是以1为首项，以1为公差的等差数列，
∴xn=n，
∵
| T3 |
| T1 |
| 10 |
| 3 |
| T4 |
| T2 |
∴数列{xn}不是“和谐数列”．
点评：本题考查数列的通项公式的求法，考查“和谐数列”的判断，是中档题，解题时要认真审题，注意构造法的合理运用．
练习册系列答案
相关题目
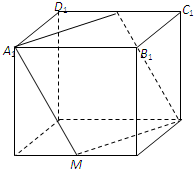在棱长为a的正方体ABCD-A1B1C1D1中，M是棱AB的中点，过A1，M，C三点的平面交棱C1D1于N点，
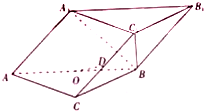三棱柱ABC-A1B1C1中，平面A1ABB1⊥平面ABC，O是AB的中点．