题目内容
若函数f（x）的定义域是[-6，2]，则函数y=f（
）的定义域 ．
| x |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数f（x）的定义域是[-6，2]，得到x的范围，从而求出函数y=f（
）的定义域．
| x |
解答：
解：∵函数f（x）的定义域是[-6，2]，
∴0≤
≤2，∴0≤x≤4，
故答案为：[0，4]．
∴0≤
| x |
故答案为：[0，4]．
点评：本题考查了函数的定义域问题，考查了二次根式的性质，是一道基础题．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
复数
为纯虚数，则实数a=（ ）
| a+i |
| 2-i |
| A、-2 | ||
B、-
| ||
| C、2 | ||
D、
|
命题“?x∈[0，+∞），x2-x+1≥0”的否定是（ ）
| A、?x∈[0，+∞），x2-x+1＜0 |
| B、?x∈（-∞，0），x2-x+1≥0 |
| C、?x0∈[0，+∞），x2-x+1＜0 |
| D、?x0∈[0，+∞），x2-x+1≥0 |
函数f（x）=(x-5)0+(x-2)-
的定义域是（ ）
| 1 |
| 3 |
| A、{x|x∈R且x≠5，x≠2} |
| B、{x|x＞2} |
| C、{x|x＞5} |
| D、{x|2＜x＜5或x＞5} |
设集合A={x|y=lg（x-1）}，B={y|y=2x，x∈R}，则A∪B=（ ）
| A、∅ | B、R |
| C、（1，+∞） | D、（0，+∞） |
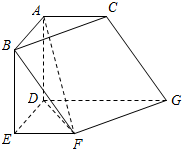在如图所示的几何体中，四边形ABED是矩形，四边形ADGC是梯形，AD⊥平面DEFG，EF∥DG，∠EDG=120°．AB=AC=FE=1，DG=2．