题目内容
14．下列函数是偶函数的是（ ）| A． | y=x2，x∈[0，1] | B． | y=x3 | C． | y=2x2-3 | D． | y=x |
分析 利用偶函数的性质判断即可．
解答 解：A、y=x2，x∈[0，1]，图象不关于y轴对称，不是偶函数；
B、f（-x）=（-x）3=-x3=-f（x），此函数为奇函数；
C、f（-x）=2×（-x）2-3=2x2-3=f（x），此函数为偶函数；
D、f（-x）=-f（x），此函数为奇函数，
故选：C．
点评 此题考查了函数奇偶性的判断，熟练掌握偶函数的定义是解本题的关键．
练习册系列答案
相关题目
3．在△ABC中，给出下列三个不等式：$\overrightarrow{AB}$$•\overrightarrow{AC}$＞0，$\overrightarrow{BA}$$•\overrightarrow{BC}$＞0，$\overrightarrow{CA}$$•\overrightarrow{CB}$＞0，其中，能够成立的不等式（ ）
| A． | 至多1个 | B． | 有且仅有1个 | C． | 至多2个 | D． | 至少2个 |
5．设x∈R，若函数f（x）=ex-ln2，则f′（0）=（ ）
| A． | -ln2 | B． | 1-ln2 | C． | 4 | D． | 1 |
2．已知f（x）=$\left\{\begin{array}{l}{{2}^{x}+3，x＞0}\\{x-1，x≤0}\end{array}\right.$，则f（1）=（ ）
| A． | 5 | B． | 0 | C． | -5 | D． | 4 |
9．已知$\frac{tanα}{tanα-1}=-1$，则$\frac{sinα-3cosα}{sinα+cosα}$=（ ）
| A． | $-\frac{5}{3}$ | B． | 3 | C． | $-\frac{3}{4}$ | D． | $\frac{1}{2}$ |
19．下列函数是正态分布密度函数的是（ ）
| A． | f（x）=$\frac{1}{{\sqrt{2π}σ}}{e^{\frac{{{{（x-r）}^2}}}{2σ}}}$ | B． | f（x）=$\frac{{\sqrt{2π}}}{2π}{e^{-\frac{x^2}{2}}}$ | ||
| C． | f（x）=$\frac{1}{{2\sqrt{2}π}}{e^{\frac{{{{（x-1）}^2}}}{4}}}$ | D． | f（x）=$\frac{1}{{\sqrt{2π}}}{e^{\frac{x^2}{2}}}$ |
6．已知全集U=R，A={x|x＞1}，B={x|x＜0}，则集合（∁UA）∩（∁UB）=（ ）
| A． | {x|x≥0} | B． | {x|x≤1} | C． | {x|0＜x＜1} | D． | {x|0≤x≤1} |
3．已知向量$\overrightarrow{a}$=（3，-2，1），$\overrightarrow{b}$=（-2，4，0），则4$\overrightarrow{a}$+2$\overrightarrow{b}$等于（ ）
| A． | （16，0，4） | B． | （8，0，4） | C． | （8，16，4） | D． | （8，-16，4） |
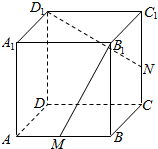如图所示，在正方体ABCD-A1B1C1D1中，M，N分别是线段AB，CC1的中点，∨MB1P的顶点P在棱CC1与棱C1D1上运动，有以下四个命题：