题目内容
9．已知$\frac{tanα}{tanα-1}=-1$，则$\frac{sinα-3cosα}{sinα+cosα}$=（ ）| A． | $-\frac{5}{3}$ | B． | 3 | C． | $-\frac{3}{4}$ | D． | $\frac{1}{2}$ |
分析 由条件利用同角三角函数的基本关系，求得tanα的值，可得要求式子的值．
解答 解：∵已知$\frac{tanα}{tanα-1}=-1$，∴tanα=$\frac{1}{2}$，则$\frac{sinα-3cosα}{sinα+cosα}$=$\frac{tanα-3}{tanα+1}$=$\frac{-\frac{5}{2}}{\frac{3}{2}}$=-$\frac{5}{3}$，
故选：A．
点评 本题主要考查同角三角函数的基本关系，属于基础题．
练习册系列答案
相关题目
20．△ABC的斜二测直观图△A′B′C′如图所示，则△ABC的面积为（ ）
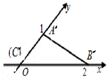
| A． | 1 | B． | 2 | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\sqrt{2}$ |
4．椭圆$\frac{x^2}{4}+{y^2}$=1上的点P到上顶点距离的最大值为（ ）
| A． | 2 | B． | $\sqrt{5}$ | C． | $\frac{{4\sqrt{3}}}{3}$ | D． | 不存在最大值 |
14．下列函数是偶函数的是（ ）
| A． | y=x2，x∈[0，1] | B． | y=x3 | C． | y=2x2-3 | D． | y=x |
1．已知直线l在x轴上的截距为3，在y轴上的截距为-2，则l的方程为（ ）
| A． | 3x-2y-6=0 | B． | 2x-3y+6=0 | C． | 2x-3y-6=0 | D． | 3x-2y+6=0 |
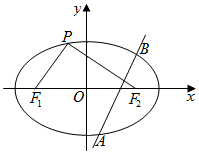已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F1、F2，离心率e=$\frac{{\sqrt{2}}}{2}$，P为椭圆E上的任意一点（不含长轴端点），且△PF1F2面积的最大值为2．