题目内容
2．已知空间四边形OABC，M，N分别是对边OA，BC的中点，点G在线段MN上，且，设$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$，则x，y，z的值分别是（ ）| A． | x=$\frac{1}{3}$，y=$\frac{1}{3}$，z=$\frac{1}{3}$ | B． | x=$\frac{1}{3}$，y=$\frac{1}{3}$，z=$\frac{1}{6}$ | C． | x=$\frac{1}{3}$，y=$\frac{1}{6}$，z=$\frac{1}{3}$ | D． | x=$\frac{1}{6}$，y=$\frac{1}{3}$，z=$\frac{1}{3}$ |
分析 利用向量的三角形法则和共线定理、平行四边形法则即可得出．
解答 
解：如图所示，
∵$\overrightarrow{OG}$=$\overrightarrow{OM}$+$\overrightarrow{MG}$=$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{ON}$-$\frac{2}{3}$$\overrightarrow{OM}$=$\frac{1}{6}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$，
又有$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$，
∴x=$\frac{1}{6}$，y=$\frac{1}{3}$，z=$\frac{1}{3}$，
故选：D．
点评 本题考查了向量的三角形法则和共线定理、平行四边形法则，属于基础题．
练习册系列答案
相关题目
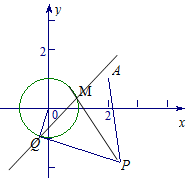已知圆O：x2+y2=1和定点A（2，1），由圆O外一点P（a，b）向圆O引切线PQ，PM，切点为Q，M，且满足|PQ|=|PA|．
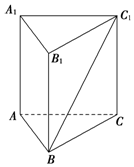如图所示，在正三棱柱ABC-A1B1C1中，AA1=6，异面直线BC1与AA1所成角的大小为30°，求该三棱柱的体积．
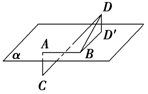如图所示，已知线段AB在平面α内，线段AC⊥α，线段BD⊥AB，线段DD′⊥α于D′，如果∠DBD=30°，AB=AC=BD=1，则CD的长为2．
14．已知函数f（x）=x-2sinx，则$f（{-\frac{π}{6}}）、f（{-1}）、f（{{{log}_3}1.2}）$的大小关系为（ ）
| A． | $f（{{{log}_3}1.2}）＞f（{-\frac{π}{6}}）＞f（{-1}）$ | B． | $f（{-\frac{π}{6}}）＞f（{{{log}_3}1.2}）＞f（{-1}）$ | ||
| C． | $f（{-\frac{π}{6}}）＞f（{-1}）＞f（{{{log}_3}1.2}）$ | D． | $f（{-1}）＞f（{-\frac{π}{6}}）＞f（{{{log}_3}1.2}）$ |