题目内容
4.已知y=f(x)是定义在R上的增函数且为奇函数,若对任意的x,y∈R,不等式f(x2-6x+21)+f(y2-8y)<0恒成立,则当x>3时,x2+y2的取值范围是( )| A. | (3,7) | B. | (9,25) | C. | (13,49) | D. | (9,49) |
分析 由函数y=f(x)为奇函数,f(x2-6x+21)+f(y2-8y)<0恒成立,可把问题转化为(x-3)2+(y-4)2<4,借助于的有关知识可求.
解答  解:∵函数y=f(x)为奇函数,定义在R上的增函数且f(x2-6x+21)+f(y2-8y)<0恒成立
解:∵函数y=f(x)为奇函数,定义在R上的增函数且f(x2-6x+21)+f(y2-8y)<0恒成立
∴f(x2-6x+21)<-f(y2-8y)=f(8y-y2)恒成立,
∴x2-6x+21<8y-y2,
∴(x-3)2+(y-4)2<4恒成立,
设M (x,y),则当x>3时,M表示以(3,4)为圆心2为半径的右半圆内的任意一点,
则d=$\sqrt{{x}^{2}+{y}^{2}}$表示区域内的点和原点的距离.
由下图可知:d的最小值是OA=$\sqrt{13}$,
OB=OC+CB,5+2=7,
当x>3时,x2+y2的范围为(13,49).
故选:C.
点评 本题考查了函数的奇偶性、单调性及圆的有关知识,解决问题的关键是把“数”的问题转化为“形”的问题,借助于图形的几何意义减少了运算量,体现“数形结合:及”转化”的思想在解题中的应用.

练习册系列答案
相关题目
14.已知集合A={-1,0,1},B={x|-1≤x≤1},则A∩B=( )
| A. | {-1,0,1} | B. | {x|-1≤x≤1} | C. | {-1,0} | D. | {0,1} |
15.已知二次函数y=x2+bx+c的图象过(1,0)与(3,0),则此函数的单调减区间为( )
| A. | (2,+∞) | B. | (-∞,2) | C. | (3,+∞) | D. | (-∞,3) |
19.设M=2a2-4a,N=a2-2a-3,则有( )
| A. | M<N | B. | M≤N | C. | M>N | D. | M≥N |
9.函数$f(x)=\sqrt{{x^2}+4x-12}$的单调减区间为( )
| A. | [-2,+∞) | B. | (-∞,-2] | C. | (-∞,-6] | D. | [2,+∞) |
14.已知函数f(x)=x-2sinx,则$f({-\frac{π}{6}})、f({-1})、f({{{log}_3}1.2})$的大小关系为( )
| A. | $f({{{log}_3}1.2})>f({-\frac{π}{6}})>f({-1})$ | B. | $f({-\frac{π}{6}})>f({{{log}_3}1.2})>f({-1})$ | ||
| C. | $f({-\frac{π}{6}})>f({-1})>f({{{log}_3}1.2})$ | D. | $f({-1})>f({-\frac{π}{6}})>f({{{log}_3}1.2})$ |
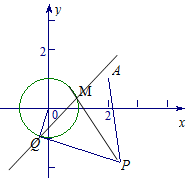 已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,PM,切点为Q,M,且满足|PQ|=|PA|.
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,PM,切点为Q,M,且满足|PQ|=|PA|.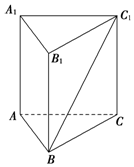 如图所示,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为30°,求该三棱柱的体积.
如图所示,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为30°,求该三棱柱的体积.