题目内容
18.在直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(3,$\frac{π}{2}$),点B的极坐标为(6,$\frac{π}{6}$),曲线C:(x-1)2+y2=1(1)求曲线C和直线AB的极坐标方程;
(2)过点O的射线l交曲线C于M点,交直线AB于N点,若|OM||ON|=2,求射线l所在直线的直角坐标方程.
分析 (1)求出A、B的直角坐标,求出直线AB的极坐标方程,根y=ρsinα,x=ρcosθ求出C的极坐标方程即可;
(2)设射线l:θ=α,分别代入曲线C的方程和直线AB的方程,得到关于α的方程,求出tanα的值,从而求出答案.
解答 解:(1)A、B的直角坐标分别是A(0,3),B(3$\sqrt{3}$,3),
故直线AB的极坐标方程是ρsinθ=3,
曲线C化为极坐标为ρ=2cosθ;
(2)设射线l:θ=α,代入曲线C得:ρM=2cosα,
代入直线AB得:ρM=$\frac{3}{sinα}$,
依题意得$\frac{3}{sinα}$•2cosα=2,解得:tanα=3.…(8分)
所以射线l所在直线的直角坐标方程为:y=3x…(10分)
点评 本题考查了直角坐标和极坐标的转化,考查求直线方程问题,是一道中档题.

练习册系列答案
相关题目
8.设P是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)上一点,双曲线的一条渐近线方程为3x-2y=0,F1,F2分别是双曲线的左、右焦点,若|PF1|=5,则|PF2|=( )
| A. | 1或9 | B. | 6 | C. | 9 | D. | 以上都不对 |
9.函数$f(x)=\sqrt{{x^2}+4x-12}$的单调减区间为( )
| A. | [-2,+∞) | B. | (-∞,-2] | C. | (-∞,-6] | D. | [2,+∞) |
6.已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A. | 若m∥n,m⊥α,则n⊥α | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,m∥β,则α∥β | D. | 若m∥α,α⊥β,则m⊥β |
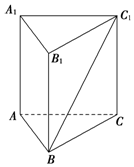 如图所示,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为30°,求该三棱柱的体积.
如图所示,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为30°,求该三棱柱的体积.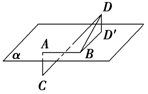 如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α于D′,如果∠DBD=30°,AB=AC=BD=1,则CD的长为2.
如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α于D′,如果∠DBD=30°,AB=AC=BD=1,则CD的长为2.