题目内容
15.由曲线y=$\frac{1}{x}$,y2=x与直线x=2,y=0围成的图形面积为$\frac{4\sqrt{2}}{3}$-ln2-$\frac{2}{3}$.分析 先求出曲线y2=x和直线y=$\frac{1}{x}$的交点坐标,从而得到积分的上下限,然后利用定积分表示出图形面积,最后根据定积分的定义求出即可.
解答 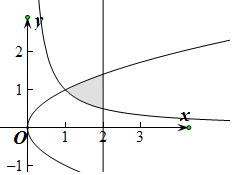 解:由曲线y2=x和直线y=$\frac{1}{x}$,解得曲线y=$\frac{1}{x}$,y2=x的交点坐标为:(1,1),
解:由曲线y2=x和直线y=$\frac{1}{x}$,解得曲线y=$\frac{1}{x}$,y2=x的交点坐标为:(1,1),
∴由曲线y=$\frac{1}{x}$,y2=x与直线x=2,y=0围成的图形面积为
S=${∫}_{1}^{2}$($\sqrt{x}$-$\frac{1}{x}$)dx=($\frac{2}{3}$x${\;}^{\frac{3}{2}}$-lnx)|${\;}_{1}^{2}$=($\frac{4\sqrt{2}}{3}$-ln2)-($\frac{2}{3}$-ln1)=$\frac{4\sqrt{2}}{3}$-ln2-$\frac{2}{3}$,
故答案为:$\frac{4\sqrt{2}}{3}$-ln2-$\frac{2}{3}$.
点评 本题主要考查了定积分在求面积中的应用,以及会利用定积分求图形面积的能力.应用定积分求平面图形面积时,积分变量的选取是至关重要的,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.△ABC中,若sin(A+B)sin(A-B)=sin2C,则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
4.执行如图所示的程序框图,输出的结果S=( )


| A. | 9 | B. | 15 | C. | 20 | D. | 38 |





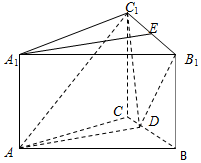 如图,在正三棱柱ABC-A1B1C1中,点D为为边BC的中点,AB=4,AA1=2.
如图,在正三棱柱ABC-A1B1C1中,点D为为边BC的中点,AB=4,AA1=2.