题目内容
7.执行如图所示的程序框图,则输出的S=11.
分析 由已知中的程序框图,可知:该程序的功能是计算并输出变量S的值,模拟程序的运行过程,分析出各变量的变化情况,可得答案.
解答 解:模拟程序的运行,可得:
k=1,S=0
不满足条件k>7,执行循环体,S=1,k=3
不满足条件k>7,执行循环体,S=4,k=7
不满足条件k>7,执行循环体,S=11,k=15
此时,满足条件k>7,退出循环,输出S的值为11,
故答案为:11.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.

练习册系列答案
相关题目
17.下列写法中正确的是( )
| A. | 0∈∅ | B. | 0∪∅={∅} | C. | 0⊆∅ | D. | ∅⊆{0} |
2.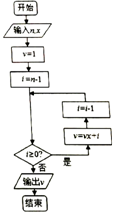 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )| A. | 12 | B. | 15 | C. | 25 | D. | 50 |
12. 已知程序框图如图,则输出的i的值是( )
已知程序框图如图,则输出的i的值是( )
 已知程序框图如图,则输出的i的值是( )
已知程序框图如图,则输出的i的值是( )| A. | 19 | B. | 20 | C. | 21 | D. | 22 |
19. 美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算,他们创造了优良的计数系统,其中开平方算法是最具有代表性的.程序框图如图所示,若输入a,n,ξ的值分别为8,2,0.5,(每次运算都精确到小数点后两位)则输出结果为( )
美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算,他们创造了优良的计数系统,其中开平方算法是最具有代表性的.程序框图如图所示,若输入a,n,ξ的值分别为8,2,0.5,(每次运算都精确到小数点后两位)则输出结果为( )
 美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算,他们创造了优良的计数系统,其中开平方算法是最具有代表性的.程序框图如图所示,若输入a,n,ξ的值分别为8,2,0.5,(每次运算都精确到小数点后两位)则输出结果为( )
美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算,他们创造了优良的计数系统,其中开平方算法是最具有代表性的.程序框图如图所示,若输入a,n,ξ的值分别为8,2,0.5,(每次运算都精确到小数点后两位)则输出结果为( )| A. | 2.81 | B. | 2.82 | C. | 2.83 | D. | 2.84 |
4.定义在R上的函数f(x)满足f(x)+f′(x)>2,ef(1)=2e+4,则不等式f(x)>$\frac{4}{{e}^{x}}$+2(其中e为自然对数的底数)的解集为( )
| A. | (1,+∞) | B. | (-∞,0)∪(1,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,1) |
5.已知集合A={x|x2-2x≤0},B={x|x≤a},若A⊆B,则实数a的取值范围是( )
| A. | a≥2 | B. | a>2 | C. | a<0 | D. | a≤0 |