题目内容
8.无穷数列1,3,6,10…的通项公式为( )| A. | an=$\frac{{{n^2}+n}}{2}$ | B. | an=$\frac{{{n^2}-n}}{2}$ | C. | an=n2-n+1 | D. | an=n2+n+1 |
分析 仔细观察数列1,3,6,10…,便可发现其中的规律:第n项应该为1+2+3+4+…+n=$\frac{n(n+1)}{2}$,便可求出数列的通项公式
解答 解:仔细观察数列1,3,6,10,可以发现:
1=1
3=1+2
6=1+2+3
10=1+2+3+4
…
∴第n项为1+2+3+4+…+n=$\frac{n(n+1)}{2}$,
∴数列1,3,6,10,15…的通项公式为an=$\frac{n(n+1)}{2}$=$\frac{{n}^{2}+n}{2}$
故选:A
点评 本题考查了数列的基本知识,考查了学生的计算能力和观察能力,解题时要认真审题,仔细解答,避免错误,属于基础题.

练习册系列答案
相关题目
18.已知等差数列{an}的前n项和为Sn,且2S3-3S2=15,则数列{an}的公差为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
19.圆${C_1}:{x^2}+{y^2}+2x+2y-2=0$与圆${C_2}:{x^2}+{y^2}-4x-2y+4=0$的公切线有( )
| A. | .1条 | B. | .2条 | C. | .3条 | D. | .4条 |
16.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=( )
| A. | 2 | B. | $\sqrt{6}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
12.若$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a-\overrightarrow b}|=2|{\overrightarrow a}|$,则向量$\overrightarrow a-\overrightarrow b$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
9.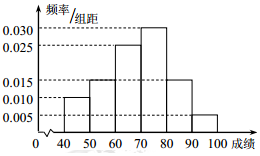 在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).
在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).
(1)求a的值,并计算所抽取样本的平均值$\overline x$(同一组中的数据用该组区间的中点值作代表);
(2)填写下面的2×2列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?
附表及公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
 在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).
在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).(1)求a的值,并计算所抽取样本的平均值$\overline x$(同一组中的数据用该组区间的中点值作代表);
(2)填写下面的2×2列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?
| 文科生 | 理科生 | 合计 | |
| 获奖 | 5 | ||
| 不获奖 | |||
| 合计 | 200 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
