题目内容
16.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=( )| A. | 2 | B. | $\sqrt{6}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
分析 利用两个向量数量积的定义与模长公式,进行计算即可.
解答 解:平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=2×1×cos120°=-1.
∴${(\overrightarrow{a}+2\overrightarrow{b})}^{2}$=${\overrightarrow{a}}^{2}$+4$\overrightarrow{a}$•$\overrightarrow{b}$+4${\overrightarrow{b}}^{2}$
=22+4×(-1)+4×12
=4,
∴|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2.
故选:A.
点评 本题主要考查两个向量数量积的定义与求向量的模应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.在正方体ABCD-A1B1C1D1中,直线AB1与平面ABC1D1所成的角的正弦值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
8.无穷数列1,3,6,10…的通项公式为( )
| A. | an=$\frac{{{n^2}+n}}{2}$ | B. | an=$\frac{{{n^2}-n}}{2}$ | C. | an=n2-n+1 | D. | an=n2+n+1 |
18.已知函数f(x)的定义域为[0,2],则函数f(x-3)的定义域为( )
| A. | [-3,-1] | B. | [0,2] | C. | [2,5] | D. | [3,5] |
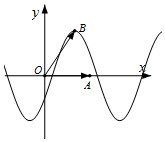 直角坐标系xOy中,已知点A(1,0),函数f(x)=sin(2x-$\frac{π}{6}$)的图象在y轴右侧的第一个最高点为B,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{π}{3}$.
直角坐标系xOy中,已知点A(1,0),函数f(x)=sin(2x-$\frac{π}{6}$)的图象在y轴右侧的第一个最高点为B,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{π}{3}$.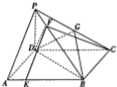 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.