题目内容
17. 在四棱锥P-ABCD中,底面ABCD为矩形,AP⊥平面PCD,E,F分别为PC,AB的中点.求证:
在四棱锥P-ABCD中,底面ABCD为矩形,AP⊥平面PCD,E,F分别为PC,AB的中点.求证:(1)平面PAD⊥平面ABCD;
(2)EF∥平面PAD.
分析 (1)利用线面垂直的性质可证AP⊥CD,又ABCD为矩形,AD⊥CD,利用线面垂直的判定定理可证CD⊥平面PAD,利用面面垂直的判定可证平面PAD⊥平面ABCD.
(2)连接AC,BD交于点O,连接OE,OF,由ABCD为矩形,O点为AC中点,可证OE∥PA,进而可证OE∥平面PAD,同理可得:OF∥平面PAD,通过证明平面OEF∥平面PAD,即可证明EF∥平面PAD.
解答 证明:(1)∵AP⊥平面PCD,CD?平面PCD,
∴AP⊥CD,
∵ABCD为矩形,∴AD⊥CD,…2分
又∵AP∩AD=A,AP?平面PAD,AD?平面PAD,
∴CD⊥平面PAD,…4分
∵CD?平面ABCD,
∴平面PAD⊥平面ABCD…6分
(2)连接AC,BD交于点O,连接OE,OF,
∵ABCD为矩形,∴O点为AC中点,
∵E为PC中点,
∴OE∥PA,
∵OE?平面PAD,PA?平面PAD,
∴OE∥平面PAD,…8分
同理可得:OF∥平面PAD,…10分
∵OE∩OF=O,
∴平面OEF∥平面PAD,…12分
∵EF?平面OEF,
∴EF∥平面PAD…14分
点评 本题主要考查了线面垂直的判定和性质,面面垂直的判定,线面平行的判定与面面平行的性质的综合应用,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
9.若直线2x-y+2=0与直线y=kx+1平行,则实数k的值为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
6.“-1≤x≤2”是“x2-x-2=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 冲要条件 | D. | 既不充分也不必要条件 |
6.函数f(x)=$\frac{{e}^{2x}}{x}$的导函数为( )
| A. | f′(x)=2e2x | B. | f′(x)=$\frac{(2x-1){e}^{2x}}{{x}^{2}}$ | C. | f′(x)=$\frac{2{e}^{2x}}{x}$ | D. | f′(x)=$\frac{(x-1){e}^{2x}}{{x}^{2}}$ |
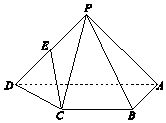 如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1
如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1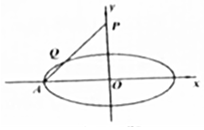 如图,过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点A作直线交y轴于点P,交椭圆于点Q,若△AOP是等腰三角形,且$\overrightarrow{PQ}$=2$\overrightarrow{QA}$,则椭圆的离心率是$\frac{2\sqrt{5}}{5}$.
如图,过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点A作直线交y轴于点P,交椭圆于点Q,若△AOP是等腰三角形,且$\overrightarrow{PQ}$=2$\overrightarrow{QA}$,则椭圆的离心率是$\frac{2\sqrt{5}}{5}$.