题目内容
14.函数f(x)=x+lg(x-2)的零点所在区间为( )| A. | (2,2.0001) | B. | (2.0001,2.001) | C. | (2.001,2.01) | D. | (2.01,3) |
分析 由函数零点的存在性定理,结合答案直接代入计算取两端点函数值异号的即可.
解答 解:f(2.001)=2.001+lg(2.001-2)=2.001-3<0,f(2.01)=2.001+lg(2.01-2)=2.01-2>0,
由函数零点的存在性定理,函数ff(x)=x+lg(x-2)的零点所在的区间为(2.001,2.01)
故选:C
点评 本题考查函数零点的判定定理的应用,属基础知识、基本运算的考查.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
4.诚信是立身之本,道德之基.某校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“
$\frac{周实际回收水费}{周投入成本}$”表示每周“水站诚信度”.为了便于数据分析,以四周为一个周期,下表为该水站连续八周(共两个周期)的诚信度数据统计,如表1:
(Ⅰ)计算表1中八周水站诚信度的平均数$\overline{x}$
(Ⅱ)从表1诚信度超过91% 的数据中,随机抽取2个,求至少有1个数据出现在第二个周期的概率;
(Ⅲ)学生会认为水站诚信度在第二个周期中的后两周出现了滑落,为此学生会举行了“以诚信为本”主题教育活动,并得到活动之后一个周期的水站诚信度数据,如表2:
请根据提供的数据,判断该主题教育活动是否有效,并根据已有数据说明理由.
$\frac{周实际回收水费}{周投入成本}$”表示每周“水站诚信度”.为了便于数据分析,以四周为一个周期,下表为该水站连续八周(共两个周期)的诚信度数据统计,如表1:
| 第一周 | 第二周 | 第三周 | 第四周 | |
| 第一个周期 | 95% | 98% | 92% | 88% |
| 第二个周期 | 94% | 94% | 83% | 80% |
(Ⅱ)从表1诚信度超过91% 的数据中,随机抽取2个,求至少有1个数据出现在第二个周期的概率;
(Ⅲ)学生会认为水站诚信度在第二个周期中的后两周出现了滑落,为此学生会举行了“以诚信为本”主题教育活动,并得到活动之后一个周期的水站诚信度数据,如表2:
| 第一周 | 第二周 | 第三周 | 第四周 | |
| 第三个周期 | 85% | 92% | 95% | 96% |
9.若直线2x-y+2=0与直线y=kx+1平行,则实数k的值为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
19.下列函数满足在定义域上为减函数且为奇函数的是( )
| A. | y=cos2x | B. | y=lg|x| | C. | y=-x | D. | y=$\frac{1}{x}$ |
6.“-1≤x≤2”是“x2-x-2=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 冲要条件 | D. | 既不充分也不必要条件 |
3.如果一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面积和球的表面积之比为( )
| A. | 9:4 | B. | 4:3 | C. | 3:1 | D. | 3:2 |
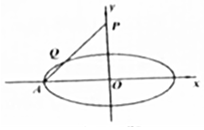 如图,过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点A作直线交y轴于点P,交椭圆于点Q,若△AOP是等腰三角形,且$\overrightarrow{PQ}$=2$\overrightarrow{QA}$,则椭圆的离心率是$\frac{2\sqrt{5}}{5}$.
如图,过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点A作直线交y轴于点P,交椭圆于点Q,若△AOP是等腰三角形,且$\overrightarrow{PQ}$=2$\overrightarrow{QA}$,则椭圆的离心率是$\frac{2\sqrt{5}}{5}$.