题目内容
9.已知$f(x)={x^2}-1,g(x)=\left\{\begin{array}{l}x-1\;(x≥0)\\ 2-x\;(x<0)\end{array}\right.$(1)求g[f(x)];
(2)设F(x)=max{f(x),g(x)},作函数F(x)的图象,并由此求出F(x)的最小值.
分析 (1)对f(x)的值进行讨论,迭代;
(2)分段求出F(x)的解析式,作出图象,得出最小值.
解答 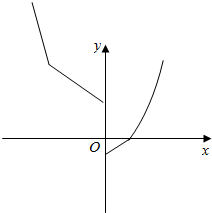 解:(1)当x2-1≥0,即x≤-1,或x≥1时,g[f(x)]=x2-1-1=x2-2,
解:(1)当x2-1≥0,即x≤-1,或x≥1时,g[f(x)]=x2-1-1=x2-2,
当x2-1<0,即-1<x<1时,g[f(x)]=2-(x2-1)=-x2+3.
∴g[f(x)]=$\left\{\begin{array}{l}{{x}^{2}-2,x≤-1或x≥1}\\{-{x}^{2}+3,-1<x<1}\end{array}\right.$.
(2)令h(x)=f(x)-g(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x≥0}\\{{x}^{2}+x-3,x<0}\end{array}\right.$,
当x≥0时,令x2-x≥0,解得x≥1,令x2-x<0,解得0<x<1.
当x<0时,令x2+x-3≥0,解得x≤$\frac{-1-\sqrt{13}}{2}$,令x2+x-3<0,解得$\frac{-1-\sqrt{13}}{2}$<x<0,
∴F(x)=$\left\{\begin{array}{l}{{x}^{2}-1,x≥1或x≤\frac{-1-\sqrt{13}}{2}}\\{x-1,0≤x<1}\\{2-x,\frac{-1-\sqrt{13}}{2}<x<0}\end{array}\right.$.
函数图象如图所示:
∴F(x)的最小值是-1.
点评 本题考查了不等式的解法,分段函数的图象及应用.

练习册系列答案
相关题目
17.点E、F分别是三棱锥P-ABC的棱AP、BC的中点,AB=6,PC=8,EF=5,则异面直线AB与PC所成的角为( )
| A. | 60° | B. | 45° | C. | 30° | D. | 90° |
4.方程$a=sin(2x+\frac{π}{3}),x∈[0,\frac{π}{2}]$上有解,则实数a的取值范围( )
| A. | [-1,1] | B. | $[-\frac{{\sqrt{3}}}{2},\frac{{\sqrt{3}}}{2}]$ | C. | $[-\frac{{\sqrt{3}}}{2},1]$ | D. | [0,1] |
14.若函数$f(x)=sinωx-\sqrt{3}cosωx$,ω>0,x∈R,又f(x1)=2,f(x2)=0,且|x1-x2|的最小值为$\frac{3π}{2}$,则ω的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | 2 |
1.已知$\overrightarrow i$和$\overrightarrow j$是互相垂直的单位向量,向量$\overrightarrow{a_n}$满足:$\overrightarrow i•\overrightarrow{a_n}=n$,$\overrightarrow j•\overrightarrow{a_n}=2n+1$,n∈N*,设θn为$\overrightarrow i$和$\overrightarrow{a_n}$的夹角,则( )
| A. | θn随着n的增大而增大 | B. | θn随着n的增大而减小 | ||
| C. | 随着n的增大,θn先增大后减小 | D. | 随着n的增大,θn先减小后增大 |