Question

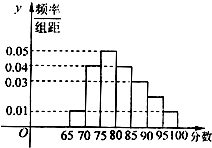如图为某校语言类专业N名毕业生的综合测评成绩（百分制）分布直方图，已知80～90分数段的学员数为21人
（Ⅰ）求该专业毕业总人数N和90～95分数段内的人数n；
（Ⅱ）现欲将90～95分数段内的n名毕业生分配往甲、乙、丙三所学校，若向学校甲分配两名毕业生，且其中至少有一名男生的概率为

3

5

，求n名毕业生中男女各几人（男女人数均至少两人）？
（Ⅲ）在（Ⅱ）的结论下，设随机变量ξ表示n名毕业生中分配往乙学校的三名学生中男生的人数，求ξ的分布列和数学期望．

Answer 1

考点：离散型随机变量及其分布列,频率分布直方图,离散型随机变量的期望与方差

专题：概率与统计

分析：（Ⅰ）先求出其不意80～90分数段的毕业生的频率，再求出毕业生的总人数，由此利用90～95分数段内的人数频率，从而能求出90～95分数段内的人数．
（Ⅱ）90：95分数段内共6名毕业生，设其中男生z名，女生为6-x名设分配往甲校的两名毕业生中至少有一名男毕业生为事件A，由P（A）=1-

C 2 6-x

C 2 6

=

3

5

，能求出6名毕业生中有男生2人，女生4人．
（Ⅲ）ξ表示n名毕业生中分配往甲学校的两名学生中男生的人数，ξ的取值可以为0，1，2，分别求出相应的概率，由此能求出ξ的分布列和随机变量ξ数学期望．

解答： 解：（Ⅰ）80～90分数段的毕业生的频率为：
p₁=（0.04+0.03）×5=0.35，
此分数段的学员总数为21人，
∴毕业生的总人数N为N=

21

0.35

=60，
90～95分数段内的人数频率为：
p₂=1-（0.01+0.04+0.05+0.04+0.03+0.01）×5=0.1，
∴90～95分数段内的人数n=60×0.1=6．
（Ⅱ）90：95分数段内共6名毕业生，设其中男生z名，女生为6-x名
设分配往甲校的两名毕业生中至少有一名男毕业生为事件A，
则P（A）=1-

C 2 6-x

C 2 6

=

3

5

，
解得x=2或x=9（舍去），
即6名毕业生中有男生2人，女生4人．…（8分）
（Ⅲ）ξ表示n名毕业生中分配往甲学校的两名学生中男生的人数，
所以ξ的取值可以为0，1，2，
当ξ=0时，P（ξ=0）=

C 3 4

C 3 6

=

1

5

，
当ξ=1时，P（ξ=1）=

C 1 2 C 2 4

C 3 6

=

3

5

，
当ξ=2时，P（ξ=2）=

C 2 2 C 1 4

C 3 6

=

1

5

，
所以ξ的分布列为

ξ	0	1	2
P	1 5	3 5	1 5

所以随机变量ξ数学期望为Eξ=0×

1

5

+1×

3

5

+2×

1

5

=1．…（12分）

点评：本题考查频率直方图的应用，考查离散型随机变量的分布列和数学期望的求法，解题时要认真审题，是中档题．