题目内容
 如图所示,正方体ABCD-A1B1C1D1中,E、F分别是BB1,D1B1的中点,棱长为1,求点E、F的坐标和B1关于原点D对称的点的坐标.
如图所示,正方体ABCD-A1B1C1D1中,E、F分别是BB1,D1B1的中点,棱长为1,求点E、F的坐标和B1关于原点D对称的点的坐标.考点:空间中的点的坐标
专题:空间向量及应用
分析:利用正方体的结构特征和空间向量的基本性质求解.
解答:
解:∵正方体ABCD-A1B1C1D1中,
E、F分别是BB1,D1B1的中点,棱长为1,
∴E(1,1,
)、F(
,
,1),B1(1,1,1),
∴B1关于原点D对称的点的坐标为(-1,-1,-1).

E、F分别是BB1,D1B1的中点,棱长为1,
∴E(1,1,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴B1关于原点D对称的点的坐标为(-1,-1,-1).
点评:本题考查空间中点的坐标的求法,是基础题,解题时要认真审题,注意正方体的结构特征的合理运用.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
某射手在一次射击中,射中10环、9环、8环的概率分别是0.20,0.30,0.20,则此射手在一次射击中不足8环的概率为( )
| A、0.40 | B、0.30 |
| C、0.60 | D、0.90 |
方程log2x+x-2=0的解所在的区间为( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
若sinA=
,则sin(6π-A)的值为( )
| 1 |
| 3 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
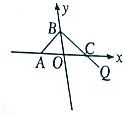 如图,已知A(-3p,0)(p>0),B,C两点分别在y轴和x轴上运动,并且满足
如图,已知A(-3p,0)(p>0),B,C两点分别在y轴和x轴上运动,并且满足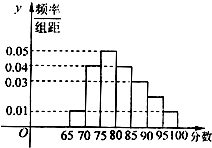 如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人
如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人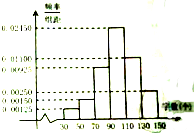 重庆Z中学为筹备参加“汉字听写比赛”,对初二年级的400名同学进行了一次摸底听写比赛,每位同学听写150个字,听写正确130个字以上(含130个)的同学才可以参加市级决赛.
重庆Z中学为筹备参加“汉字听写比赛”,对初二年级的400名同学进行了一次摸底听写比赛,每位同学听写150个字,听写正确130个字以上(含130个)的同学才可以参加市级决赛.