题目内容
在等比数列{an}中,an>0(n∈N*),且a1a3=4,a3+1是a2和a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=log2an+2,求满足方程
+
+…+
=
的n的值.
(1)求数列{an}的通项公式;
(2)若bn=log2an+2,求满足方程
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
| 25 |
| 51 |
考点:数列的求和,数列的应用,数列与函数的综合
专题:等差数列与等比数列
分析:(1)由a1a3=4,a3+1是a2和a4的等差中项,结合等差数列的性质及通项公式可求q,a1,从而可求通项
(2)由已知可求bn,结合等差数列的求和公式及二次函数的性质可求Sn的最小值.
(2)由已知可求bn,结合等差数列的求和公式及二次函数的性质可求Sn的最小值.
解答:
解:(1)由已知a1a3=4得,a22=4,2(a2q+1)=a2+a2q2,
∵an>0,∴a2=2,2(2q+1)=2+2q2
∴q=2,a1=1
∴an=2n-1,
(2)bn=log2an+2=n+1,
=
=
-
,
由
+
+…+
=
,
可得:
-
+
-
+…+
-
=
即
-
=
,
解得:n=100.
∵an>0,∴a2=2,2(2q+1)=2+2q2
∴q=2,a1=1
∴an=2n-1,
(2)bn=log2an+2=n+1,
| 1 |
| bnbn+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
由
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
| 25 |
| 51 |
可得:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 25 |
| 51 |
即
| 1 |
| 2 |
| 1 |
| n+2 |
| 25 |
| 51 |
解得:n=100.
点评:本题考查等比数列的通项公式的求法,数列求和的方法,数列与函数相结合,考查分析问题解决问题的能力.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知α:x≥a,β:x2-2x-3≤0,若α是β的必要不充分条件,则实数a的取值范围为( )
| A、[0,+∞) |
| B、(-∞,-1] |
| C、[-1,+∞) |
| D、(1,3] |
已知三棱锥D-ABC的三个侧面与底面全等,且AB=AC=
,BC=2,则二面角A-BC-D的大小为( )
| 3 |
A、arccos
| ||||
B、arccos
| ||||
C、
| ||||
D、
|
某射手在一次射击中,射中10环、9环、8环的概率分别是0.20,0.30,0.20,则此射手在一次射击中不足8环的概率为( )
| A、0.40 | B、0.30 |
| C、0.60 | D、0.90 |
函数y=2sin2x的图象可看成是由y=sinx的图象按下列哪种变换得到的?( )
A、横坐标不变,纵坐标变为原来的
| ||
B、纵坐标变为原来的2倍,横坐标变为原来的
| ||
| C、横坐标不变,纵坐标变为原来的2倍 | ||
D、纵坐标变为原来的
|
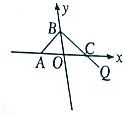 如图,已知A(-3p,0)(p>0),B,C两点分别在y轴和x轴上运动,并且满足
如图,已知A(-3p,0)(p>0),B,C两点分别在y轴和x轴上运动,并且满足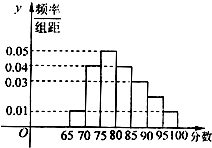 如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人
如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人