题目内容
已知不等式x2-2x-3≤0的解集为A,不等式
≥0的解集为B.
(1)求A∩B;
(2)若不等式x2+ax+b≤0的解集为A∩B,求a,b的值.
| x-2 |
| x-5 |
(1)求A∩B;
(2)若不等式x2+ax+b≤0的解集为A∩B,求a,b的值.
考点:交集及其运算,一元二次不等式的解法
专题:集合
分析:(1)解一元二次不等式求得A、解分式不等式求得B,再根据两个集合的交集的定义求得A∩B.
(2)结合题意利用由韦达定理可得
,由此解的a和b的值.
(2)结合题意利用由韦达定理可得
|
解答:
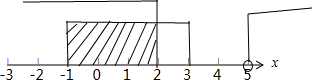 解:(1)不等式x2-2x-3≤0即 (x-3)(x+1)≤0,解得-1≤x≤3,故有A=[-1,3].
解:(1)不等式x2-2x-3≤0即 (x-3)(x+1)≤0,解得-1≤x≤3,故有A=[-1,3].
由不等式
≥0可得
,解得x≤2,或 x>5,故有B=(-∞,2]∪(5,+∞).
∴A∩B=[-1,2].
(2)若不等式x2+ax+b≤0的解集为A∩B=[-1,2],
则由韦达定理可得
,即a=-1,b=-2.
 解:(1)不等式x2-2x-3≤0即 (x-3)(x+1)≤0,解得-1≤x≤3,故有A=[-1,3].
解:(1)不等式x2-2x-3≤0即 (x-3)(x+1)≤0,解得-1≤x≤3,故有A=[-1,3].由不等式
| x-2 |
| x-5 |
|
∴A∩B=[-1,2].
(2)若不等式x2+ax+b≤0的解集为A∩B=[-1,2],
则由韦达定理可得
|
点评:本题主要考查一元二次不等式的解法、分式不等式的解法,两个集合的交集的定义,韦达定理的应用,属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知条件p:a=2,条件q:圆C1:x2+y2=9与圆C2:(x-a)2+y2=1相切,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
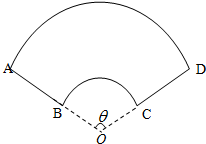 某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点O为圆心的两个同心圆弧AD、弧BC以及两条线段AB和CD围成的封闭图形.花坛设计周长为30米,其中大圆弧AD所在圆的半径为10米.设小圆弧BC所在圆的半径为x米(0<x<10),圆心角为θ弧度.
某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点O为圆心的两个同心圆弧AD、弧BC以及两条线段AB和CD围成的封闭图形.花坛设计周长为30米,其中大圆弧AD所在圆的半径为10米.设小圆弧BC所在圆的半径为x米(0<x<10),圆心角为θ弧度.