题目内容
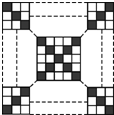 如图所示,在一个(2n-1)×(2n-1)(n∈N且n≥2)的正方形网格内涂色,要求两条对角线的网格涂黑色,其余网格涂白色.若用f(n)表示涂白色网格的个数与涂黑色网格的个数的比值,则f(n)的最小值为
如图所示,在一个(2n-1)×(2n-1)(n∈N且n≥2)的正方形网格内涂色,要求两条对角线的网格涂黑色,其余网格涂白色.若用f(n)表示涂白色网格的个数与涂黑色网格的个数的比值,则f(n)的最小值为考点:函数解析式的求解及常用方法
专题:网格型,函数的性质及应用
分析:只要数对角线上共有多小个小方格即可,注意两条对角线在正方形中心处有一个小方格是重合的.
解答:
解:由题意知在(2n-1)×(2n-1)(n∈N且n≥2)的正方形网格内对角线共2(2n-1)-1=4n-3个,即共有(4n-3)个方格涂黑色,余下的方格都涂白色,
∴f(n)=
,
∴f(n)=
=
•
=
•
=
•[(4n-3)+
-2]
令t=
,
∵n≥2,∴t∈(0,
],又y=
(t+
-2)在t∈(0,
]上单调递减,
∴当t=
,即n=2时,有最小值,f(2)=
.
故答案为:
.
∴f(n)=
| (2n-1)2-(4n-3) |
| 4n-3 |
∴f(n)=
| 4n2-8n+4 |
| 4n-3 |
| 1 |
| 4 |
| 16n2-32n+16 |
| 4n-3 |
| 1 |
| 4 |
| (4n-3)2-2(4n-3)+1 |
| 4n-3 |
| 1 |
| 4 |
| 1 |
| 4n-3 |
令t=
| 1 |
| 4n-3 |
∵n≥2,∴t∈(0,
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| t |
| 1 |
| 5 |
∴当t=
| 1 |
| 5 |
| 4 |
| 5 |
故答案为:
| 4 |
| 5 |
点评:本题是一个函数的应用题,理解题意是前提,算出对角线上小方格个数是关键,建立函数关系式,利用双勾函数的单调性就可以求出函数最小值.

练习册系列答案
相关题目
给出下列命题:
(1)p:x-2=0,q:(x-2)(x-3)=0.
(2)p:m<-2;q:方程x2-x-m=0无实根.
(3)已知四边形M,p:M是矩形;q:M的对角线相等.
试分别指出p是q的什么条件.
(1)p:x-2=0,q:(x-2)(x-3)=0.
(2)p:m<-2;q:方程x2-x-m=0无实根.
(3)已知四边形M,p:M是矩形;q:M的对角线相等.
试分别指出p是q的什么条件.
已知全集U=R,集合A={x|lgx≤0},B={x|2x≤1},则A∪B=( )
| A、(-∞,0] |
| B、(-∞,1] |
| C、[0,+∞) |
| D、[1,+∞) |