题目内容
“a＜b”是“log2a＜log2b”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据对数的基本运算和充分条件和必要条件的定义即可得到结论．
解答：
解：∵log2a＜log2b，
∴0＜a＜b，
∴“a＜b”是“log2a＜log2b”的必要不充分条件，
故选：B．
∴0＜a＜b，
∴“a＜b”是“log2a＜log2b”的必要不充分条件，
故选：B．
点评：本题主要考查充分条件和必要条件的判断，利用对数的基本运算性质是解决本题的关键，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
若函数f（x）=lg
的定义域为（-∞，1]，则有（ ）
| 1+2x+4x•a |
| 3 |
A、a＞-
| ||
B、a=-
| ||
C、a＜-
| ||
| D、a＞0 |
已知数列{an}是等差数列，且a3+a6=5，数列{bn}是等比数列，且b5=
，则b2•b8=（ ）
| a2+5a5 |
| A、1 | B、5 | C、10 | D、15 |
已知某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（ ）
A、
| ||||
| B、30cm3 | ||||
| C、40cm3 | ||||
| D、42cm3 |
函数y=
的定义域是（ ）
| log0.5(1-x) |
| A、（-∞，1） |
| B、[0，1） |
| C、[0，+∞） |
| D、[1，+∞） |
“α=
+2kπ（k∈Z）”是“cos2α=0”的（ ）
| π |
| 4 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不是充分条件也不是必要条件 |
设变量x，y满足约束条件
．目标函数z=ax+2y仅在（1，0）处取得最小值，则a的取值范围为（ ）
|
| A、（-1，2） |
| B、（-2，4） |
| C、（-4，0] |
| D、（-4，2） |
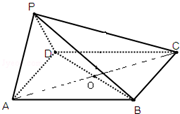如图，在四棱锥P-ABCD中，底面ABCD是边长为a的正方形，其对角线交点为O，侧面PAD⊥底面ABCD，且PA=PD=