题目内容
12.已知函数f(x)=(x+1)lnx-a(x-1),a∈R(1)若a=0时,求f(x)在x=1处的切线
(2)若函数f(x)>0 对?x∈(1,+∞)恒成立.求a的取值范围
(3)从编号为1到2015的2015个小球中,有放回地连续取16次小球 (每次取一球),记所取得的小球的号码互不相同的概率为p,求证:$\frac{1}{p}$>e${\;}^{\frac{120}{2011}}$.
分析 (1)求出导数,可得切线斜率和切点,由点斜式方程可得切线方程;
(2)由题意可得(x+1)lnx-a(x-1)>0 对x∈(1,+∞) 恒成立,即lnx-$\frac{a(x-1)}{x+1}$>0对x∈(1,+∞) 恒成立.令g(x)=lnx-$\frac{a(x-1)}{x+1}$,x∈(1,+∞),求出导数,令h(x)=x2+(2-2a)x+1,(x>1),对a讨论,求出单调性,即可得到a的范围;
(3)求出p=$\frac{2015×2014×…×2000}{201{5}^{16}}$,由2000×2014<20072,…,2006×2008<20072,运用累乘法
再由(2)得lnx>$\frac{2(x-1)}{x+1}$(x>1),令x=$\frac{2015}{2007}$,即可得证.
解答 解:(1)当a=0时,f(x)=(x+1)lnx,f(1)=0,
f′(x)=lnx+$\frac{x+1}{x}$,f′(1)=2,
所以f(x)在x=1处的切线为y-0=2(x-1),
即2x-y-2=0 …(2分)
(2)由题意(x+1)lnx-a(x-1)>0 对x∈(1,+∞) 恒成立,
即lnx-$\frac{a(x-1)}{x+1}$>0对x∈(1,+∞) 恒成立.
g(x)=lnx-$\frac{a(x-1)}{x+1}$,x∈(1,+∞),
g′(x)=$\frac{{x}^{2}+(2-2a)x+1}{x(x+1)^{2}}$,(x>1)
令h(x)=x2+(2-2a)x+1,(x>1),
①当a≤2 时,h(x)的对称轴为x=a-1≤1
则h(x) 在(1,+∞)上递增,
即h(x)>h(1)=4-2a≥0,所以g′(x)>0(x>1)恒成立,
则g(x)在(1,+∞)上递增,g(x)>g(1)=0恒成立,符合要求;
②a>2时,△=(2-2a)2-4=4a(a-2)>0,
且h(1)=4-2a<0,则h(x)=0(x>1)有唯一根x=x0,
则x∈(1,x0)时,h(x)<0,g′(x)<0,
则g(x)在(1,x0)上递减,
即有?x∈(1,x0),g(x)<g(1)=0,
这与g(x)>0(x>1)恒成立矛盾.舍去.
综上:a≤2…(8分)
(3)p=$\frac{2015×2014×…×2000}{201{5}^{16}}$,
由2000×2014<20072,…,2006×2008<20072,
可得p=$\frac{2015×2014×…×2000}{201{5}^{16}}$<$\frac{200{7}^{15}}{201{5}^{15}}$,
又由(2)得lnx>$\frac{2(x-1)}{x+1}$(x>1),
则ln$\frac{2015}{2007}$>$\frac{2(\frac{2015}{2007}-1)}{\frac{2015}{2007}+1}$=$\frac{8}{2011}$,
则$\frac{2015}{2007}$>e${\;}^{\frac{8}{2011}}$,($\frac{2015}{2007}$)15>e${\;}^{\frac{120}{2011}}$
故$\frac{1}{p}$>($\frac{2015}{2007}$)15>e${\;}^{\frac{120}{2011}}$…(12分)
点评 本题考查导数的运用:求单调区间和极值、最值,考查不等式恒成立问题解法和不等式证明,注意运用转化思想和构造函数法,属于难题.

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | 36 | B. | 48 | C. | 72 | D. | 120 |
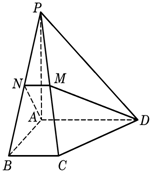 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点. 如图,椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和双曲线C2:$\frac{{x}^{2}}{4}$-y2=1有公共顶点A,B,P,Q分别在C1,C2且异于A,B点.直线AP,BP,AQ,BQ的斜率分别为k1,k2,k3,k4且k1+k2+k3+k4=0.
如图,椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和双曲线C2:$\frac{{x}^{2}}{4}$-y2=1有公共顶点A,B,P,Q分别在C1,C2且异于A,B点.直线AP,BP,AQ,BQ的斜率分别为k1,k2,k3,k4且k1+k2+k3+k4=0.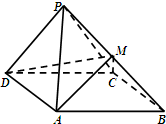 如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,∠ADC=60°,点P在底面ABCD上的射影为△ACD的重心,点M为线段PB上的点.
如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,∠ADC=60°,点P在底面ABCD上的射影为△ACD的重心,点M为线段PB上的点.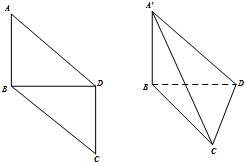 如图,在平行四边形ABCD中,AB=BD=DC=1,AD=BC=$\sqrt{2}$,将平行四边形ABCD沿对角线BD折成三棱锥A′-BCD,使平面A′BD⊥平面BCD,在下列结论中:
如图,在平行四边形ABCD中,AB=BD=DC=1,AD=BC=$\sqrt{2}$,将平行四边形ABCD沿对角线BD折成三棱锥A′-BCD,使平面A′BD⊥平面BCD,在下列结论中: