题目内容
7.函数f(x)=x3+ax2+3x-1在x=-3时取得极值,则a=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 因为f(x)在x=-1时取极值,则求出f′(x)得到f′(-3)=0,解出求出a即可.
解答 解:∵f′(x)=3x2+2ax+3,f(x)在x=-3时取得极值,
∴f′(-3)=30-6a=0
∴a=5.
经验证a=5时,函数f(x)=x3+5x2+3x-1在x=-3时取得极值,满足题意.
故选:D.
点评 本题考查学生利用导数研究函数极值的能力,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
15.已知函数f(x)=cos($\frac{π}{2}$+x)+sin2($\frac{π}{2}$+x),x∈R,则f(x)的最大值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{4}$ | C. | 1 | D. | 2$\sqrt{2}$ |
2.函数f(x)=x|x+a|+b是奇函数的充要条件是( )
| A. | ab=0 | B. | a+b=0 | C. | a2+b2=0 | D. | a=b |
17.已知函数f(x)=2-x2,g(x)=x.若f(x)*g(x)=min{f(x),g(x)},那么,f(x)*g(x)的最大值是( )(注:min表示最小值)
| A. | 2 | B. | 1 | C. | 0 | D. | $-\frac{1}{2}$ |
 ,则
,则 ( )
( ) B.
B.
 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.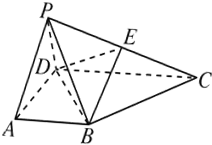 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.