题目内容
17. 如图,椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和双曲线C2:$\frac{{x}^{2}}{4}$-y2=1有公共顶点A,B,P,Q分别在C1,C2且异于A,B点.直线AP,BP,AQ,BQ的斜率分别为k1,k2,k3,k4且k1+k2+k3+k4=0.
如图,椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和双曲线C2:$\frac{{x}^{2}}{4}$-y2=1有公共顶点A,B,P,Q分别在C1,C2且异于A,B点.直线AP,BP,AQ,BQ的斜率分别为k1,k2,k3,k4且k1+k2+k3+k4=0.(1)求证:O,P,Q共线.
(2)设F1,F2分别为C1,C2的右焦点,PF1∥QF2,求k12+k22+k32+k42的值.
分析 (1)设P(x1,y1),Q(x2,y2),根据直线的斜率公式建立斜率过程结合向量关系的坐标公式进行证明即可.
(2)求出椭圆和双曲线的焦点坐标,结合PF1∥QF2,得到坐标之间的关系,利用直线的斜率公式进行化简求解即可.
解答 解:(1)设P(x1,y1),Q(x2,y2),则
k1+k2+k3+k4=$\frac{{y}_{1}}{{x}_{1}+2}$+$\frac{{y}_{1}}{{x}_{1}-2}$+$\frac{{y}_{2}}{{x}_{2}+2}$+$\frac{{y}_{2}}{{x}_{2}-2}$=$\frac{2{y}_{1}{y}_{1}}{{{x}_{1}}^{2}-4}$+$\frac{2{x}_{2}{y}_{2}}{{{x}_{2}}^{2}-4}$ …(2分)
又x12-4=-4y12,x22-4=-4y22,
所以k1+k2+k3+k4=$\frac{2{x}_{1}{y}_{2}}{-4{y}_{1}^{2}}$+$\frac{2{x}_{2}{y}_{2}}{4{y}_{2}^{2}}$=$\frac{{x}_{2}}{2{y}_{2}}-\frac{{x}_{1}}{2{y}_{1}}$=$\frac{{y}_{1}{x}_{2}-{y}_{2}{x}_{1}}{2{y}_{1}{y}_{2}}$…(4分)
由k1+k2+k3+k4=0得y1x2-y2x1=0
即$\overrightarrow{OP}∥\overrightarrow{OQ}$,
所以O、P、Q三点共线 …(6分)
(2)由题意得F1($\sqrt{3}$,0),F2($\sqrt{5}$,0),由PF1∥QF2知|OP|:|OQ|=$\sqrt{3}:\sqrt{5}$,
因为O、P、Q三点共线,所以$\frac{{x}_{1}^{2}}{{x}_{2}^{2}}=\frac{3}{5}$ …①…(7分)
设直线PQ的斜率为k,则$\left\{\begin{array}{l}{\frac{{x}_{1}^{2}}{4}+{k}^{2}{{x}_{1}}^{2}=1}\\{\frac{{x}_{2}^{2}}{4}-{k}^{2}{{x}_{2}}^{2}=1}\end{array}\right.$得($\frac{1}{4}$+k2)x12=($\frac{1}{4}$-k2)x22,…②
由①②得k2=$\frac{1}{16}$ …(10分),
又k1k2=$\frac{{y}_{1}^{2}}{{x}_{1}^{2}-4}$=$\frac{{y}_{1}^{2}}{-4{y}_{1}^{2}}$=-$\frac{1}{4}$,k3k4=$\frac{{y}_{2}^{2}}{{x}_{2}^{2}-4}$=$\frac{{y}_{2}^{2}}{4{y}_{2}^{2}}$=$\frac{1}{4}$ …(12分)
从而k12+k22+k32+k42=(k1+k2)2+(k3+k4)2-2(k1k2+k3k4)=2(k1+k2)2=2×($\frac{2{x}_{2}{y}_{2}}{-4{y}_{1}^{2}}$)2=$\frac{1}{2}×(\frac{{x}_{1}}{{y}_{1}})^{2}=\frac{1}{2}×\frac{1}{{k}^{2}}$=8…(13分)
点评 本题主要考查圆锥曲线的综合问题,利用直线的斜率公式以及向量和直线平行的公式进行转化是解决本题的关键.考查学生的计算能力.

 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2)求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+a,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间?参考公式:
b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
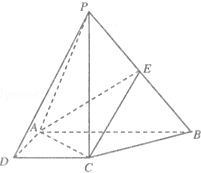 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点. 如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为45°,又AC=1,BC=2PM=2,∠ACB=90°.
如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为45°,又AC=1,BC=2PM=2,∠ACB=90°.