题目内容
2.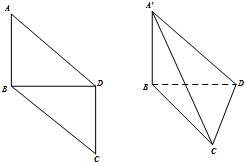 如图,在平行四边形ABCD中,AB=BD=DC=1,AD=BC=$\sqrt{2}$,将平行四边形ABCD沿对角线BD折成三棱锥A′-BCD,使平面A′BD⊥平面BCD,在下列结论中:
如图,在平行四边形ABCD中,AB=BD=DC=1,AD=BC=$\sqrt{2}$,将平行四边形ABCD沿对角线BD折成三棱锥A′-BCD,使平面A′BD⊥平面BCD,在下列结论中:①直线CD⊥平面A′BD;
②平面A′BC⊥平面BCD;
③点B到平面A'CD的距离为$\frac{{\sqrt{2}}}{4}$;
④棱A′C上存在一点到顶点A'、B、C、D的距离相等.
所有正确结论的编号是①②④.
分析 根据面面垂直的性质定理,可判断①;根据面面垂直的判定定理,可判断②;利用等体积法,求出点B到平面A'CD的距离,可判断③;根据直角三角形的性质,可判断④.
解答 解:∵在平行四边形ABCD中,AB=BD=DC=1,AD=BC=$\sqrt{2}$,
∴AB⊥BD,BD⊥CD,
将平行四边形ABCD沿对角线BD折成三棱锥A′-BCD后,
∵平面A′BD⊥平面BCD,
∴直线CD⊥平面A′BD;
故①正确;
同理:A′B⊥平面BCD,
由A′B?平面A′BC得:
平面A′BC⊥平面BCD,
故②正确;
棱锥A′-BCD的体积V=$\frac{1}{3}$×$\frac{1}{2}$×1×1×1=$\frac{1}{6}$,
△A'CD的面积S=$\frac{\sqrt{2}}{2}$,
设点B到平面A'CD的距离为h,则$\frac{1}{3}$×$\frac{\sqrt{2}}{2}$h=$\frac{1}{6}$,
解得:h=$\frac{\sqrt{2}}{2}$,
故③错误;
棱A′C的中点到顶点A'、B、C、D的距离相等.
故④正确;
故答案为:①②④
点评 本题以命题的真假判断与应用为载体,考查了棱锥的结构特征,平面与平面垂直的判定与性质,等体积法,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知函数f(x)=2-x2,g(x)=x.若f(x)*g(x)=min{f(x),g(x)},那么,f(x)*g(x)的最大值是( )(注:min表示最小值)
| A. | 2 | B. | 1 | C. | 0 | D. | $-\frac{1}{2}$ |
11.函数y=x2-2x+1在闭区间[0,3]上的最大值和最小值之和为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |



