有6个座位连成一片排.现有3人入座.则恰有两个空位相邻的不同坐法的种数是( )A．36B．48C．72D．120 题目和参考答案——青夏教育精英家教网——

题目内容

4．有6个座位连成一片排，现有3人入座，则恰有两个空位相邻的不同坐法的种数是（　　）

A．

36

B．

48

C．

72

D．

120

分析先求出3个人在6个位置的所有坐法，再减去空座各不相邻的坐法和三个空座相邻的坐法得答案．

解答解：3人坐6个座位，坐法共有A₆³，
其中空坐各不相邻的坐法为C₄³A₃³，
三个空坐相连的坐法C₄¹A₃³，
∴满足条件的坐法共有A₆³-C₄³A₃³-C₄¹A₃³=72．
故选：C．

点评本题考查排列与组合问题，考查了插空排列，是中档题．

练习册系列答案

智能考核卷系列答案

活力试卷系列答案

琢玉计划系列答案

小学全能测试卷系列答案

名校全优考卷系列答案

课课优能力培优100分系列答案

期末迎考特训系列答案

高效课时100系列答案

小学生百分易卷系列答案

帮你学系列答案

相关题目

14．学校体育队共有5人，其中会打排球的有2人，会打乒乓球的有5人，现从中选2人．设ξ为选出的人中既会打排球又会打乒乓球的人数，则随机变量ξ的均值E（ξ）=（　　）

15．已知函数f（x）=cos（$\frac{π}{2}$+x）+sin²（$\frac{π}{2}$+x），x∈R，则f（x）的最大值为（　　）

12．已知函数f（x）=（x+1）lnx-a（x-1），a∈R
（1）若a=0时，求f（x）在x=1处的切线
（2）若函数f（x）＞0 对?x∈（1，+∞）恒成立．求a的取值范围
（3）从编号为1到2015的2015个小球中，有放回地连续取16次小球（每次取一球），记所取得的小球的号码互不相同的概率为p，求证：$\frac{1}{p}$＞e${\;}^{\frac{120}{2011}}$．

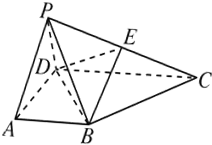已知在四棱锥P-ABCD中，底面ABCD是直角梯形，∠BAD=90°，2AB=2AD=CD，侧面PAD是正三角形且垂直于底面ABCD，E是PC的中点．
（1）求证：BE⊥平面PCD；
（2）求二面角B-PC-D的正弦值．

9．已知向量$\overrightarrow a$，$\overrightarrow b$满足|$\overrightarrow a$|=2|$\overrightarrow b$|≠0，且函数在f（x）=$\frac{1}{3}{x^3}+\frac{1}{2}|\overrightarrow a|{x^2}$$+（\overrightarrow a•\overrightarrow b）x$在R上有极值，则向量$\overrightarrow a$，$\overrightarrow b$的夹角的取值范围是（$\frac{π}{3}$，π）．

16．已知函数$f（x）=lnx-\frac{1}{2}x$．
（Ⅰ）求f（x）的图象在点（1，f（1））处的切线方程；
（Ⅱ）当x＞1时，$f（x）+\frac{a}{x}＜0$恒成立，求实数a的取值范围；
（Ⅲ）证明：当n∈N^*且n≥2时，$\frac{1}{2ln2}+\frac{1}{3ln3}+…+\frac{1}{nlnn}＞\frac{{3{n^2}-n-2}}{{2{n^2}+2n}}$．

13．已知y=f′（x）是函数y=f（x）的导数，将y=f（x）和y=f′（x）的图象画在同一个直角坐标系中，不可能正确的是（　　）

14．在直角坐标系xOy中，F₁，F₂分别为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左、右焦点，点P在椭圆上，若△POF₂是面积为$\sqrt{3}$的正三角形，则椭圆的离心率为$\sqrt{3}$-1．