题目内容
2．已知函数f（x）=x3-3ax2-bx，其中a，b为实数，若f（x）在x=1处取得的极值为2，求a，b的值．分析 根据f（x）在x=1处取得的极值为2，可建立关于a，b的两个等式关系，解方程组即可．
解答 解：函数f（x）=x3-3ax2-bx，可得f′（x）=3x2-6ax-b，由题设可知：f'（1）=0且f（1）=2，
即$\left\{\begin{array}{l}{3-6a-b=0}\\{1-3a-b=2}\end{array}\right.$，
解得a=$\frac{4}{3}$，b=-5．
点评 本小题主要考查函数的导数与极值，考查综合利用数学知识分析问题、解决问题的能力，属于基础题．
练习册系列答案
相关题目
，则
（ ）
B．
14．学校体育队共有5人，其中会打排球的有2人，会打乒乓球的有5人，现从中选2人．设ξ为选出的人中既会打排球又会打乒乓球的人数，则随机变量ξ的均值E（ξ）=（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{4}{5}$ | D． | 1 |
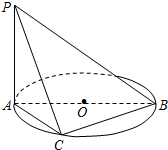已知PA垂直于以AB为直径的ΘO所在的平面，C是ΘO上异于A，B的动点，PA=1，AB=2，当三棱锥P-ABC取得最大体积时，求：