题目内容
3．在1，2，3，…，9这9个自然数中，任取3个不同的数．（1）组成三位数“abc”，若满足a＜b＞c的三位数叫做凸数，这样的凸三位数有多少个？
（2）设X为所取3个数中奇数的个数，求随机变量X的概率分布列及数学期望．
分析 （1）从9个自然数中，任取3个不同的数，共有${C}_{9}^{3}$=84种等可能的结果，由条件得最大的在中间，其它两个排两边，有2种排法，由此能求出这样的三位数的个数．
（2）由题意得X的取值范围为0，1，2，3，分别求出相应的概率，由此能求出随机变量X的分布列和数学期望．
解答 解：（1）从9个自然数中，任取3个不同的数，共有${C}_{9}^{3}$=84种等可能的结果…（2分）
由条件得最大的在中间，其它两个排两边，有2种排法，…（4分）
所以这样的三位数共有$C_9^3×2=84×2=168$个．…（6分）
（2）由题意得X的取值范围为0，1，2，3，…（7分）
P（X=0）=$\frac{C_5^0C_4^3}{C_9^3}=\frac{1}{21}$，P（X=1）=，
P（X=2）=$\frac{C_5^2C_4^1}{C_9^3}=\frac{10}{21}$，P（X=3）=$\frac{C_5^3C_4^0}{C_9^3}=\frac{5}{42}$，
∴随机变量X的分布列为：
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{21}$ | $\frac{5}{14}$ | $\frac{10}{21}$ | $\frac{5}{42}$ |
（算对1个给（1分），不列表格或只列表格照样给分）
EX=$0×\frac{1}{21}+1×\frac{5}{14}+2×\frac{10}{21}+3×\frac{5}{42}=\frac{5}{3}$…（13分）
点评 本题考查排列组合数的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
14．学校体育队共有5人，其中会打排球的有2人，会打乒乓球的有5人，现从中选2人．设ξ为选出的人中既会打排球又会打乒乓球的人数，则随机变量ξ的均值E（ξ）=（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{4}{5}$ | D． | 1 |
11．
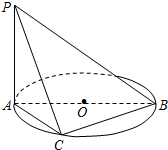已知PA垂直于以AB为直径的ΘO所在的平面，C是ΘO上异于A，B的动点，PA=1，AB=2，当三棱锥P-ABC取得最大体积时，求：
（1）PC与AB所成角的大小；
（2）PA与面PCB所成角的大小．
已知PA垂直于以AB为直径的ΘO所在的平面，C是ΘO上异于A，B的动点，PA=1，AB=2，当三棱锥P-ABC取得最大体积时，求：（1）PC与AB所成角的大小；
（2）PA与面PCB所成角的大小．
已知在四棱锥P-ABCD中，底面ABCD是矩形，且AD=2，AB=1，PA⊥平面ABCD，E、F分别是线段AB、BC的中点．
15．已知函数f（x）=cos（$\frac{π}{2}$+x）+sin2（$\frac{π}{2}$+x），x∈R，则f（x）的最大值为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{5}{4}$ | C． | 1 | D． | 2$\sqrt{2}$ |
