题目内容
9.已知直线l的参数方程为$\left\{\begin{array}{l}x=tcosφ\\ y=-2+tsinφ\end{array}\right.$(t为参数,0≤φ<π),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=1,l与C交于不同的两点P1,P2.(1)求φ的取值范围;
(2)以φ为参数,求线段P1P2中点轨迹的参数方程.
分析 (1)求解曲线C的直角坐标方程,将直线l的参数方程$\left\{\begin{array}{l}x=tcosφ\\ y=-2+tsinφ\end{array}\right.$(t为参数,0≤φ<π),带入,得到关于t的一元二次方程的关系式,由题意判别式大于0,可得φ的取值范围.
(2)利用参数的几何意义即可求线段P1P2中点轨迹的参数方程.
解答 解:(1)曲线C的极坐标方程为ρ=1,根据ρ2=x2+y2可得曲线C的直角坐标方程为x2+y2=1,
将$\left\{\begin{array}{l}x=tcosφ\\ y=-2+tsinφ\end{array}\right.$代入x2+y2=1得t2-4tsinφ+3=0(*)
由16sin2φ-12>0,得$|{sinφ}|>\frac{{\sqrt{3}}}{2}$,又0≤φ≤π,
∴所求φ的取值范围是$({\frac{π}{3},\frac{2π}{3}})$;
(Ⅱ)由(1)中的(*)可知,$\frac{{{t_1}+{t_2}}}{2}=2sinφ$,代入$\left\{\begin{array}{l}x=tcosφ\\ y=-2+tsinφ\end{array}\right.$中,
整理:得P1P2的中点的轨迹方程为$\left\{\begin{array}{l}x=sin2φ\\ y=-1-cos2φ\end{array}\right.$(φ为参数,$\frac{π}{3}<φ<\frac{2π}{3}$).
故得线段P1P2中点轨迹的参数方程为为$\left\{\begin{array}{l}x=sin2φ\\ y=-1-cos2φ\end{array}\right.$(φ为参数,$\frac{π}{3}<φ<\frac{2π}{3}$).
点评 本题主要考查了极坐标方程与直角坐标方程的互换和参数方程的几何意义的运用.

 快捷英语周周练系列答案
快捷英语周周练系列答案| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 1 | D. | 0 |

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 36秒 | B. | 33秒 | C. | 30秒 | D. | 15秒 |
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{3}}}{4}$ | D. | $\frac{{3\sqrt{3}}}{8}$ |
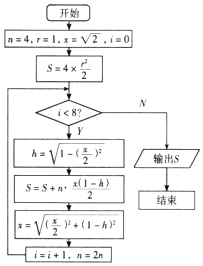 我国魏晋时期的数学家刘徽,他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π,用刘徽自己的原话就是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.”设计程序框图是计算圆周率率不足近似值的算法,其中圆的半径为1.请问程序中输出的S是圆的内接正( )边形的面积.
我国魏晋时期的数学家刘徽,他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π,用刘徽自己的原话就是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.”设计程序框图是计算圆周率率不足近似值的算法,其中圆的半径为1.请问程序中输出的S是圆的内接正( )边形的面积.