题目内容
4.已知元素为实数的集合S满足下列条件:①0∉S,1∉S;②若a∈S,则$\frac{1}{1-a}$∈S.(1)已知2∈S,试求出S中的其它所有元素;
(2)若{3,-3}⊆S,求使元素个数最少的集合S;
(3)若非空集合S为有限集,则你对集合S的元素个数有何猜测?并请证明你的猜测正确.
分析 (1)由2∈S,能推导出S中的其它所有元素为-1,$\frac{1}{2}$.
(2)3∈S,推导出现-$\frac{1}{2}$∈S,$\frac{2}{3}$∈S,由-3∈S,推导出$\frac{1}{4}$∈S,$\frac{4}{3}$∈S,由此能示出使{3,-3}?S的元素个数最少的集合S.
(3)设a∈S,则{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$}?S,若b∈S,而b∉{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$},则{b,$\frac{1}{1-b}$,$\frac{b-1}{b}$}?S,且{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$}∩{b,$\frac{1}{1-b}$,$\frac{b-1}{b}$}=∅,若b,$\frac{1}{1-b}$,$\frac{b-1}{b}$中有元素∈{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$},则{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$,b,$\frac{1}{1-b}$,$\frac{b-1}{b}$}?S,由此能证明S的元素个数为3的倍数.
解答 解:(1)∵2∈S,∴$\frac{1}{1-2}$=-1∈S,$\frac{1}{1-(-1)}$=$\frac{1}{2}$∈S,$\frac{1}{1-\frac{1}{2}}=2$∈S.
∴S中的其它所有元素为-1,$\frac{1}{2}$.
(2)3∈S,$\frac{1}{1-3}$=-$\frac{1}{2}$∈S,
$\frac{1}{1-(-\frac{1}{2})}=\frac{2}{3}∈S$,$\frac{1}{1-\frac{2}{3}}$=3∈S,
-3∈S,$\frac{1}{1-(-3)}$=$\frac{1}{4}∈S$,$\frac{1}{1-\frac{1}{4}}$=$\frac{4}{3}∈S$,
$\frac{1}{1-\frac{4}{3}}$=-3∈S,
∴使{3,-3}?S的元素个数最少的集合S为{-3,-$\frac{1}{2}$,$\frac{1}{4}$,$\frac{2}{3}$,$\frac{4}{3}$,3}.
(3)设a∈S,则a≠0,1且a∈S,$\frac{1}{1-a}$∈S,$\frac{1}{1-\frac{1}{1-a}}$=$\frac{a-1}{a}$∈S,$\frac{1}{1-\frac{a-1}{a}}$=a∈S(*)
由于a=$\frac{1}{1-a}$,即a2-a+1=0(a≠1),但a2-a+1=0无实数根
故a≠$\frac{1}{1-a}$,同理$\frac{1}{1-a}≠\frac{a-1}{a}$,$\frac{a-1}{a}≠a$,∴{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$}?S,
若存在b∈S,而b∉{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$},则{b,$\frac{1}{1-b}$,$\frac{b-1}{b}$}?S,且{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$}∩{b,$\frac{1}{1-b}$,$\frac{b-1}{b}$}=∅,
若b,$\frac{1}{1-b}$,$\frac{b-1}{b}$中有元素∈{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$},
则利用前述的(*)式可知b∈{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$}
于是{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$,b,$\frac{1}{1-b}$,$\frac{b-1}{b}$}?S,
上述推理还可继续,由于S为有限集,故上述推理有限步可中止
∴S的元素个数为3的倍数.
点评 本题考查集合元素的求法,考查集合中元素个数的判断与证明,是中档题,解题时要认真审题,注意集合中元素性质的合理运用.

| A. | -4 | B. | -7 | C. | 1 | D. | 6 |
| A. | $2\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
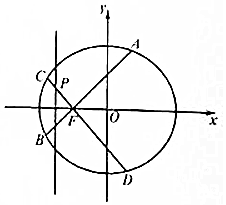 如图,已知F为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点,过点F且互相垂直的两条直线分别交椭圆于A、B及C、D.
如图,已知F为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点,过点F且互相垂直的两条直线分别交椭圆于A、B及C、D.