题目内容
1.已知双曲线$C:{x^2}-\frac{y^2}{3}=1$的右顶点为A,过右焦点F的直线l与C的一条渐近线平行,交另一条渐近线于点B,则S△ABF=( )| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{3}}}{4}$ | D. | $\frac{{3\sqrt{3}}}{8}$ |
分析 根据题意,由双曲线的方程可得a、b的值,进而可得c的值,可以确定A、F的坐标,设BF的方程为y=$\sqrt{3}$(x-2),代入y=-$\sqrt{3}$x,解得B的坐标,由三角形的面积公式,计算可得答案.
解答 解:由双曲线$C:{x^2}-\frac{y^2}{3}=1$,
可得a2=1,b2=3,故c=$\sqrt{{a}^{2}+{b}^{2}}$=2,
∴A(1,0),F(2,0),渐近线方程为y=±$\sqrt{3}$x,
不妨设BF的方程为y=$\sqrt{3}$(x-2),
代入方程y=-$\sqrt{3}$x,解得:B(1,-$\sqrt{3}$).
∴S△AFB=$\frac{1}{2}$|AF|•|yB|=$\frac{1}{2}$•1•$\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
故选:B.
点评 本题考查双曲线方程的运用,注意运用渐近线方程,关键求出B的坐标;解此类面积的题目时,注意要使三角形的底或高与坐标轴平行或重合,以简化计算.

练习册系列答案
相关题目
13.若双曲线mx2+2y2=2的虚轴长为4,则该双曲线的焦距为( )
| A. | $2\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
10.掷一枚均匀的硬币3次,出现正面向上的次数恰好为两次的概率为( )
| A. | $\frac{3}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{5}{8}$ | D. | $\frac{1}{2}$ |
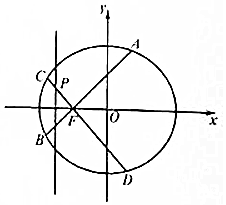 如图,已知F为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点,过点F且互相垂直的两条直线分别交椭圆于A、B及C、D.
如图,已知F为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点,过点F且互相垂直的两条直线分别交椭圆于A、B及C、D.