题目内容
设二次函数f(x)=ax2-2ax+c在区间[0,1]上单调递减,且f(m)≤f(0),则实数m的取值范围是( )
A.(-∞,0] B.[2,+∞)
C.(-∞,0]∪[2,+∞) D.[0,2]
D解析 二次函数f(x)=ax2-2ax+c在区间[0,1]上单调递减,则a≠0,f′(x)=2a(x-1)≤0,x∈[0,1],所以a>0,即函数图象的开口向上,对称轴是直线x=1.所以f(0)=f(2),则当f(m)≤f(0)时,有0≤m≤2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下表是函数值y随自变量x变化的一组数据,它最可能的函数模型是( )
| x | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 15 | 17 | 19 | 21 | 23 | 25 | 27 |
A.一次函数模型 B.幂函数模型
C.指数函数模型 D.对数函数模型
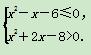
 -
-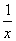 (a>0,x>0),若f(x)在
(a>0,x>0),若f(x)在 上的值域为
上的值域为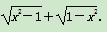 .
. B.±
B.±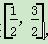 ,都有f(x)-2mx≤1成立,求实数m的取值范围.
,都有f(x)-2mx≤1成立,求实数m的取值范围.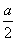 恒过定点,则这个定点的坐标是( )
恒过定点,则这个定点的坐标是( ) C.
C.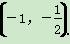 D.
D.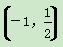
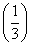 x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值( )
x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值( )