已知函数f(x)＝ax2+2x+c(a.c∈N*)满足①f(1)＝5,②6<f(2)<11. (1)求f(x)的解析式． (2)若对任意实数x∈.都有f(x)-2mx≤1成立.求实数m的取值范围．题目和参考答案——青夏教育精英家教网—

题目内容

已知函数f(x)＝ax²＋2x＋c(a，c∈N^*)满足①f(1)＝5；②6<f(2)<11.

(1)求f(x)的解析式．

(2)若对任意实数x∈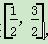，都有f(x)－2mx≤1成立，求实数m的取值范围．

解　(1)f(1)＝a＋2＋c＝5，所以c＝3－a.

又6<f(2)<11，即6<4a＋c＋4<11，

则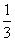－<a<，故a＝1，c＝2.

f(x)的解析式为f(x)＝x²＋2x＋2.

(2)由(1)知f(x)＝x²＋2x＋2，由题意得2(1－m)≤－上恒成立，易求＝－，

故2(1－m)≤－，解得m≥.

练习册系列答案

相关题目

已知函数f(x)＝5^|x|，g(x)＝ax²－x(a∈R)，若f[g(1)]＝1，则a＝(　　)

A．1 B．2

C．3 D．－1

已知函数f(x)在实数集R上具有下列性质：①直线x＝1是函数f(x)的一条对称轴；②f(x＋2)＝－f(x)；③当1≤x₁<x₂≤3时，[f(x₂)－f(x₁)](x₂－x₁)<0，则f(2 011)，f(2 012)，f(2 013)从大到小的顺序为________．

已知f(x)，g(x)分别是定义在R上的奇函数和偶函数，且f(x)－g(x)＝^x，则f(1)，g(0)，g(－1)之间的大小关系是________．

设二次函数f(x)＝ax²－2ax＋c在区间[0,1]上单调递减，且f(m)≤f(0)，则实数m的取值范围是(　　)

A．(－∞，0] B．[2，＋∞)

C．(－∞，0]∪[2，＋∞) D．[0,2]

设集合A＝{x||x－1|<2}，B＝{y|y＝2x，x∈[0,2]}，则A∩B＝ (　　)

A．[0,2] B．(1,3)

C．[1,3) D．(1,4)

若函数f(x)＝a^|2x－4|(a>0，a≠1)满足f(1)＝，则f(x)的单调递减区间是________．

已知f(x)＝log₄(4^x－1)．

(1)求f(x)的定义域；

(2)讨论f(x)的单调性；

(3)求f(x)在区间上的值域．

已知某食品厂生产100克饼干的总费用为1.80元，现该食品厂对饼干采用两种包装，其包装费及售价如表所示：

型号	小包装	大包装
质量	100克	300克
包装费	0.5元	0.8元
售价	3.00元	8.40元

下列说法中：

①买小包装实惠；

②买大包装实惠；

③卖3包小包装比卖1包大包装盈利多；

④卖1包大包装比卖3包小包装盈利多．

所有正确的说法是(　　)

A．①④ B．①③

C．②③ D．②④

试题分类