题目内容
9. 如图,直线l是曲线y=f(x)在x=3处的切线,f'(x)表示函数f(x)的导函数,则f(3)+f'(3)的值为$\frac{7}{3}$.
如图,直线l是曲线y=f(x)在x=3处的切线,f'(x)表示函数f(x)的导函数,则f(3)+f'(3)的值为$\frac{7}{3}$.
分析 根据导数的几何意义,f'(3)是曲线在(3,3)处的切线斜率为:f'(3)=$\frac{5-3}{0-3}$=-$\frac{2}{3}$,又f(3)=3,可得结论.
解答 解:由题意,f'(3)=$\frac{5-3}{0-3}$=-$\frac{2}{3}$,f(3)=3,
所以f(3)+f′(3)=-$\frac{2}{3}$+3=$\frac{7}{3}$,
故答案为:$\frac{7}{3}$.
点评 本题考查了导数的几何意义.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列变量关系是函数关系的是( )
| A. | 三角形的边长与面积之间的关系 | |
| B. | 等边三角形的边长与面积之间的关系 | |
| C. | 四边形的边长与面积之间的关 | |
| D. | 菱形的边长与面积之间的关 |
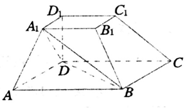 如图所示,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.
如图所示,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.