题目内容
3.已知函数f(x)满足:2f(x)•f(y)=f(x+y)+f(x-y),f(1)=$\frac{1}{2}$,且f(x)在[0,3]上单调递减,则方程f(x)=$\frac{1}{2}$在区间[-2014,2014]内根的个数为1343.分析 可令y=1,f(x)=f(x+1)+f(x-1),两次将x换为x+1,可得f(x)的周期为3,由题意可得方程的根的个数.
解答 解:2f(x)•f(y)=f(x+y)+f(x-y),f(1)=$\frac{1}{2}$,
令y=1,可得2f(x)f(1)=f(x+1)+f(x-1),
即为f(x)=f(x+1)+f(x-1),
将x换为x+1,可得f(x+1)=f(x+2)+f(x),
即有f(x+2)=f(x-1),
将x换为x+1,可得f(x+3)=f(x),
则函数f(x)以3为最小正周期的函数,
由f(1)=$\frac{1}{2}$,且f(x)在[0,3]上单调递减,
可得方程f(x)=$\frac{1}{2}$在[0,2014]之间有672个根,
在[-2014,0]之间有671个根,
则方程f(x)=$\frac{1}{2}$在区间[-2014,2014]内根的个数为672+671=1343个根.
故答案为:1343.
点评 本题考查抽象函数的性质和运用,主要是周期性的应用,考查运算能力,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
11.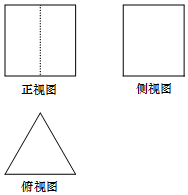 某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )
某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )
 某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )
某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $\frac{2}{3}\sqrt{3}$ | D. | 8 |
16.点B是点A(1,2,3)在坐标平面yOz内的射影,则|OB|等于( )
| A. | $\sqrt{14}$ | B. | $\sqrt{13}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
15.已知△ABC的外接圆的圆心为O,AB=2,AC=3,BC=4,则$\overrightarrow{AO}$•$\overrightarrow{BC}$=( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 7 |
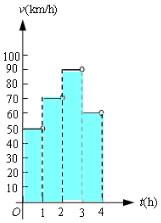 一辆汽车在某段路程中的行驶速率与时间的关系如图所示.
一辆汽车在某段路程中的行驶速率与时间的关系如图所示. 如图,直线l是曲线y=f(x)在x=3处的切线,f'(x)表示函数f(x)的导函数,则f(3)+f'(3)的值为$\frac{7}{3}$.
如图,直线l是曲线y=f(x)在x=3处的切线,f'(x)表示函数f(x)的导函数,则f(3)+f'(3)的值为$\frac{7}{3}$.