题目内容
19.已知F1,F2是椭圆$\frac{x^2}{45}+\frac{y^2}{20}=1$的两个焦点,M是椭圆上的点,且MF1⊥MF2.(1)求△MF1F2的周长;
(2)求点M的坐标.
分析 (1)根据椭圆定义,$|{M{F_1}}|+|{M{F_2}}|=2a=6\sqrt{5}$,即可求△MF1F2的周长;
(2)利用${S_{△M{F_1}{F_2}}}$=$\frac{1}{2}|{M{F_1}}|•|{M{F_2}}|=\frac{1}{2}|{{F_1}{F_2}}|•|{y_0}|$,即可求点M的坐标.
解答 解:椭圆$\frac{x^2}{45}+\frac{y^2}{20}=1$中,长半轴$a=3\sqrt{5}$,焦距$2c=2\sqrt{45-20}=10$
(1)根据椭圆定义,$|{M{F_1}}|+|{M{F_2}}|=2a=6\sqrt{5}$
所以,△MF1F2的周长为$|{{F_1}{F_2}}|+|{M{F_1}}|+|{M{F_2}}|=6\sqrt{5}+10$…(5分)
(2)设点M坐标为(x0,y0).
由MF1⊥MF2得,${|{M{F_1}}|^2}+{|{M{F_2}}|^2}={|{{F_1}{F_2}}|^2}={10^2}=100$
又${(|{M{F_1}}|+|{M{F_2}}|)^2}={(6\sqrt{5})^2}=180$
∴$|{M{F_1}}|•|{M{F_2}}|=\frac{1}{2}{[{(|{M{F_1}}|+|{M{F_2}}|)^2}-({|{M{F_1}}|^2}+{|{M{F_2}}|^2})]^2}=40$
∵${S_{△M{F_1}{F_2}}}$=$\frac{1}{2}|{M{F_1}}|•|{M{F_2}}|=\frac{1}{2}|{{F_1}{F_2}}|•|{y_0}|$,
∴|y0|=4,则|x0|=3
∴点M坐标为(3,4)或(3,-4)或(-3,4)或(-3,-4)…(12分)
点评 本题考查椭圆的方程与性质,考查椭圆的定义,考查三角形面积的计算,属于中档题.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案| A. | (0,$\frac{1}{2}$] | B. | [2,+∞) | C. | (0,2] | D. | (-∞,2] |
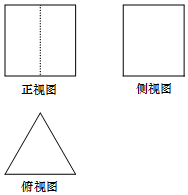 某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )
某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $\frac{2}{3}\sqrt{3}$ | D. | 8 |
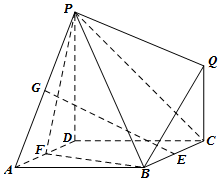 如图所示的多面体中,面ABCD是边长为2的正方形,平面PDCQ⊥平面ABCD,PD⊥DC,E,F,G分别为棱BC,AD,PA的中点.
如图所示的多面体中,面ABCD是边长为2的正方形,平面PDCQ⊥平面ABCD,PD⊥DC,E,F,G分别为棱BC,AD,PA的中点. 如图,直线l是曲线y=f(x)在x=3处的切线,f'(x)表示函数f(x)的导函数,则f(3)+f'(3)的值为$\frac{7}{3}$.
如图,直线l是曲线y=f(x)在x=3处的切线,f'(x)表示函数f(x)的导函数,则f(3)+f'(3)的值为$\frac{7}{3}$.