将正偶数集合{2.4.6.-}从小到大按第n组有2n个偶数进行分组:{2.4}.{6.8.10.12}.{14.16.18.20.22.24}.-.则2018位于( )组．A．30B．31C．32D．33 题目和参考答案——青夏教育精英家教网—

题目内容

14．将正偶数集合{2，4，6，…}从小到大按第n组有2n个偶数进行分组：{2，4}，{6，8，10，12}，{14，16，18，20，22，24}，…，则2018位于（　　）组．

A．

B．

C．

D．

分析根据题意可分析第一组、第二组、第三组、…中的数的个数及最后的数，从中寻找规律即可使问题得到解决．

解答解：第一组有2=1×2个数，最后一个数为4；
第二组有4=2×2个数，最后一个数为12即2×（2+4）；
第三组有6=2×3个数，最后一个数为24，即2×（2+4+6）；
…
∴第n组有2n个数，其中最后一个数为2×（2+4+…+2n）=4（1+2+3+…+n）=2n（n+1）．
∴当n=31时，第31组的最后一个数为2×31×32=1984，
∴当n=32时，第32组的最后一个数为2×32×33=2112，
∴2018位于第32组．
故选：C

点评本题考查数列的求和，考查观察与分析问题的能力，考查归纳法的应用，从有限项得到一般规律是难点所在，属于中档题．

练习册系列答案

5．

某种平面分形如图所示，以及分形图是有一点出发的三条线段，二级分形图是在一级分形图的每条线段的末端出发在生成两条线段，…，依次规律得到n级分形图，那么n级分形图中共有3•2ⁿ-3条线段．

2．已知函数f（x）=$\frac{3-{x}^{2}}{1+{x}^{2}}$．
（1）计算f（3），f（4），f（$\frac{1}{3}$）及f（$\frac{1}{4}$）的值；
（2）由（1）的结果猜想一个普遍的结论，并加以证明；
（3）求值f（1）+f（2）+…+f（2017）+f（$\frac{1}{2}$）+f（$\frac{1}{3}$）+…+f（$\frac{1}{2017}$）．

9．

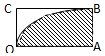如图，长方形的四个顶点坐标为O（0，0），A（4，0），B（4，2），C（0，2），曲线y=$\sqrt{x}$经过点B，现将质点随机投入长方形OABC中，则质点落在图中阴影部分的概率为（　　）

19．已知定义域为正整数集的函数f（x）=$\left\{\begin{array}{l}{\frac{1}{2}x，x为偶数}\\{x-1，x为奇数}\end{array}\right.$，f₁（x）=f（x），f_n（x）=f[f_n-1（x）]．若f_n（21）=1，则n=6；若f₄（x）=1，则x所有的值构成的集合为{7，9，10，12，16}．

6．设a=0.6^0.6，b=0.6^1.5，c=1.5^0.6，则a，b，c的大小关系（　　）

3．已知命题p：曲线C：（m+2）x²+my²=1表示双曲线，命题q：方程y²=（m²-1）x表示的曲线是焦点在x轴的负半轴上的抛物线，若p∨q为真命题，p∧q为假命题，求实数m的取值范围．

4．把函数$y=cos2x+\sqrt{3}sin2x$的图象经过变化而得到y=2sin2x的图象，这个变化是（　　）

	A．	向左平移$\frac{π}{12}$个单位		B．	向右平移$\frac{π}{12}$个单位
	C．	向左平移$\frac{π}{6}$个单位		D．	向右平移$\frac{π}{6}$个单位

试题分类