题目内容
17.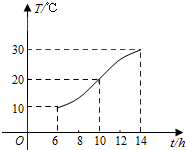 某地一天中6时至14时的温度变化曲线近似满足函数T=Asin(ωt+φ)+B(其中$\frac{π}{2}$<φ<π)6时至14时期间的温度变化曲线如图所示,它是上述函数的半个周期的图象,那么图中曲线对应的函数解析式是y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
某地一天中6时至14时的温度变化曲线近似满足函数T=Asin(ωt+φ)+B(其中$\frac{π}{2}$<φ<π)6时至14时期间的温度变化曲线如图所示,它是上述函数的半个周期的图象,那么图中曲线对应的函数解析式是y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
分析 由图中的最大值与最小值可求得b与A,由函数的周期可求得ω,由10ω+φ=2kπ,k∈Z,可求得φ.
解答 解:依题意,b=$\frac{30+10}{2}$=20,∵A>0,
∴30=A+b=A+20,
∴A=10;
又$\frac{T}{2}$=14-6=8,ω>0,
∴T=$\frac{2π}{ω}$=16,
∴ω=$\frac{π}{8}$,
∴y=f(x)=10sin($\frac{π}{8}$x+φ)+20,
又f(10)=20,
∴$\frac{π}{8}$×10+φ=2kπ,(k∈Z),
∵$\frac{π}{2}$<φ<π,
∴φ=$\frac{3π}{4}$.
∴y=f(x)=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
故答案为:y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得φ是难点,考查识图与应用的能力,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
7.已知等差数列{an}的前n项和为Sn,a1+a5=0,且a9=20.则S11=( )
| A. | 260 | B. | 220 | C. | 130 | D. | 110 |
5.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-4x,x≥1}\\{\frac{1}{x-1},x<1}\end{array}\right.$,则f(f(2))等于( )
| A. | 3 | B. | -3 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
2.化简:$\frac{1}{cosα\sqrt{1+ta{n}^{2}α}}$+$\frac{2tanα}{\sqrt{\frac{1}{cos^{2}α}-1}}$后可能取值的集合中元素的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.抛物线y=$\frac{1}{8}$x2上一点M到焦点的距离为4,则点M的纵坐标为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.在如图所示的程序框图中,当输出的T的值最大时,正整数k的值等于( )


| A. | 6 | B. | 7 | C. | 6或7 | D. | 8 |