题目内容

5．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-4x，x≥1}\\{\frac{1}{x-1}，x＜1}\end{array}\right.$，则f（f（2））等于（　　）
A．3B．-3C．$\frac{1}{5}$D．-$\frac{1}{5}$

分析 利用分段函数由里及外逐步求解即可．

解答 解：函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-4x，x≥1}\\{\frac{1}{x-1}，x＜1}\end{array}\right.$，
则f（f（2））=f（22-4×2）=f（-4）=$-\frac{1}{5}$．
故选：D．

点评 本题考查分段函数的应用，函数值的求法，是基础题．

练习册系列答案
相关题目
15．在△ABC中，内角A，B，C的对边分别为a，b，c，则“cosA=$\frac{b}{c}$”是“△ABC为Rt△”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也必要条件
16．已知a，b∈R，则“|b|+a＜0”是“b2＜a2”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
13．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$-$\overrightarrow{a}$|=1，则|$\overrightarrow{a}$+$\overrightarrow{b}$|的最大值为5．
20．已知平面直角坐标系内三点A，B，C在一条直线上，满足$\overrightarrow{OA}$=（-2，m），$\overrightarrow{OB}$=（n，1），$\overrightarrow{OC}$=（5，-1），且$\overrightarrow{OA}$⊥$\overrightarrow{OB}$，其中O为坐标原点．
（1）求实数m，n的值；
（2）设△OAC的垂心为G，且$\overrightarrow{OB}$=$\frac{3}{2}$$\overrightarrow{OG}$，试求∠AOC的大小．
10．以下叙述中正确的个数有（　　）
①为了了解高一年级605名学生的数学学习情况，打算从中抽取一个容量为30的样本，考虑用系统抽样，则分段的间隔k为30；
②函数y=ex-e-x是偶函数；
③线性回归直线方程$\stackrel{∧}{y}$=$\overline{b}$x+$\stackrel{∧}{a}$恒过（$\overline{x}$，$\overline{y}$），且至少过一个样本点；
④若f（log2x）=x+2，则f（1）=2．
A．0B．1C．2D．3
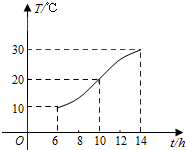17．某地一天中6时至14时的温度变化曲线近似满足函数T=Asin（ωt+φ）+B（其中$\frac{π}{2}$＜φ＜π）6时至14时期间的温度变化曲线如图所示，它是上述函数的半个周期的图象，那么图中曲线对应的函数解析式是y=10sin（$\frac{π}{8}$x+$\frac{3π}{4}$）+20，x∈[6，14]．
14．已知命题p：f（x）=$\frac{1}{2}$sinx+$\frac{1}{2}$+k（x∈R，k＞0），3≤f（x）≤6恒成立，命题q：方程$\frac{{x}^{2}}{4-k}$-$\frac{{y}^{2}}{k}$=1表示焦点在x轴上的双曲线，若p∧q为真命题，求实数k的取值范围．
15．已知数列{an}是等比数列．
（1）若a1=1，q=-2，求S8；
（2）若a1=-$\frac{3}{2}$，a4=96，求q，S4；
（3）若q=$\frac{1}{2}$，S5=$\frac{31}{8}$，求a1，a5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网