题目内容
已知数列{an}的前n项和为Sn,满足:Sn=2an-2n(n∈N*)
(1)求证:数列{an+2}是等比数列;
(2)若数列{bn}满足bn=log2(an+2),求数列{
}的前n项和Tn;
(3)(理科)若12Tn>m2-5m对所有的n∈N*恒成立,求m的取值范围.
(1)求证:数列{an+2}是等比数列;
(2)若数列{bn}满足bn=log2(an+2),求数列{
| bn |
| an+2 |
(3)(理科)若12Tn>m2-5m对所有的n∈N*恒成立,求m的取值范围.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件推导出an=2an-2an-1-2,由此能证明{an+2}是以a1+2为首项,以2为公比的等比数列.
(2)由已知条件得
=
,由此利用错位相减法能求出Tn.
(3)n=1时,Tn 取最小值T1=
-
=
,∴依题意有
>
(m2-5m)恒成立,由此能求出m的取值范围.
(2)由已知条件得
| bn |
| an+2 |
| n+1 |
| 2n+1 |
(3)n=1时,Tn 取最小值T1=
| 3 |
| 2 |
| 1+3 |
| 21+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
解答:
(1)证明:当n∈N*时,Sn=2an-2n,①
当n≥2,n∈N*时,Sn-1=2an-1-2(n-1).②
①-②,得an=2an-2an-1-2,
∴an=2an-1+2,∴an+2=2(an-1+2)
∴
=2.
当n=1时,S1=2a1-2,则a1=2,
当n=2时,a2=6,
∴{an+2}是以a1+2为首项,以2为公比的等比数列.
(2)解:由(1)知∴an+2=4•2n-1,∴an=2n+1-2.
∴bn=log2(an+2)=log22n+1=n+1,
得
=
,
则Tn=
+
+…+
,③
Tn=
+
+…+
+
,④
③-④,得
Tn=
+
+
+…+
-
=
+
-
=
+
-
-
=
-
,
∴Tn=
-
.
(3)解:∵12Tn>m2-5m对所有的n∈N*恒成立,
∴Tn>
(m2-5m)对所有的n∈N*恒成立,
∵n=1时,Tn 取最小值T1=
-
=
,
∴依题意有
>
(m2-5m)恒成立,
解得-1<m<6.
∴m的取值范围是(-1,6).
当n≥2,n∈N*时,Sn-1=2an-1-2(n-1).②
①-②,得an=2an-2an-1-2,
∴an=2an-1+2,∴an+2=2(an-1+2)
∴
| an+2 |
| an-1+2 |
当n=1时,S1=2a1-2,则a1=2,
当n=2时,a2=6,
∴{an+2}是以a1+2为首项,以2为公比的等比数列.
(2)解:由(1)知∴an+2=4•2n-1,∴an=2n+1-2.
∴bn=log2(an+2)=log22n+1=n+1,
得
| bn |
| an+2 |
| n+1 |
| 2n+1 |
则Tn=
| 2 |
| 22 |
| 3 |
| 23 |
| n+1 |
| 2n+1 |
| 1 |
| 2 |
| 2 |
| 23 |
| 3 |
| 24 |
| n |
| 2n+1 |
| n+1 |
| 2n+2 |
③-④,得
| 1 |
| 2 |
| 2 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n+1 |
| n+1 |
| 2n+1 |
=
| 1 |
| 4 |
| ||||
1-
|
| n+1 |
| 2n+2 |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n+1 |
| 2n+2 |
=
| 3 |
| 4 |
| n+3 |
| 2n+2 |
∴Tn=
| 3 |
| 2 |
| n+3 |
| 2n+1 |
(3)解:∵12Tn>m2-5m对所有的n∈N*恒成立,
∴Tn>
| 1 |
| 12 |
∵n=1时,Tn 取最小值T1=
| 3 |
| 2 |
| 1+3 |
| 21+1 |
| 1 |
| 2 |
∴依题意有
| 1 |
| 2 |
| 1 |
| 12 |
解得-1<m<6.
∴m的取值范围是(-1,6).
点评:本题考查等比数列的证明,考查数列的前n项和的求法,考查实数的取值范围的求法,解题时要认真审题,注意错位相减求和法的合理运用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
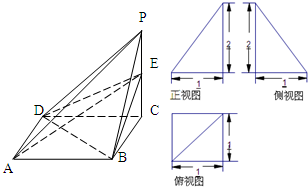 已知四棱锥P-ABCD的三视图和直观图如图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.
已知四棱锥P-ABCD的三视图和直观图如图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.