题目内容
在极坐标系中,曲线ρ=4cosθ与曲线ρ=4sinθ交于A、B两点,则A、B两点的极坐标分别为 .
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把两条曲线的极坐标方程化为直角坐标方程,求出这两条曲线的交点,再把交点坐标化为极坐标.
解答:
解:曲线方程ρ=4cosθ 即 x2+y2=4x,曲线方程ρ=4sinθ,即x2+y2=4y,
由
求得
,或
,
故两条曲线的交点A、B两点的直角坐标分别为(0,0)、(2,2),
故A、B两点的极坐标分别为(0,θ)、(2
,
),
故答案为:(0,θ)、(2
,
).
由
|
|
|
故两条曲线的交点A、B两点的直角坐标分别为(0,0)、(2,2),
故A、B两点的极坐标分别为(0,θ)、(2
| 2 |
| π |
| 4 |
故答案为:(0,θ)、(2
| 2 |
| π |
| 4 |
点评:本题主要考查点的极坐标与直角坐标的互化,求两条曲线的交点坐标,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=
的定义域是( )
| ln(x-1) |
| x-2 |
| A、(1,2) |
| B、(1,2)∪(2,+∞) |
| C、(1,+∞) |
| D、[1,2)∪(2,+∞) |
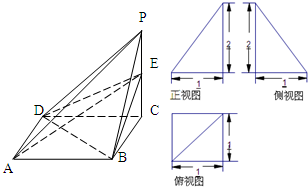 已知四棱锥P-ABCD的三视图和直观图如图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.
已知四棱锥P-ABCD的三视图和直观图如图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点. 某市高二数学期中考试中,对90分及其以上的成绩情况进行统计,其频率分布直方图如图所示,若(130,140]分数段的人数为10人,则(90,100]分数段的人数为
某市高二数学期中考试中,对90分及其以上的成绩情况进行统计,其频率分布直方图如图所示,若(130,140]分数段的人数为10人,则(90,100]分数段的人数为