题目内容
14.已知递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2,a4的等差中项.(1)求数列{an}的通项公式;
(2)若bn=log2a2n,Sn是数列{bn}的前n项和,求使Sn>40+4n成立的正整数n的最小值.
分析 (1)通过设等比数列{an}的公比为q(q>1)利用a3+2是a2,a4的等差中项可知2(a3+2)=a2+a4,结合a2+a3+a4=28可知a3=8,再次利用a2+a3+a4=28计算可知q=2,通过公式an=a3•qn-3计算即得结论;
(2)由(1)可知bn=2n,利用等差数列的求和公式计算可知Sn=n2+n,进而问题转化为求不等式n2+n>40+4n的最小正整数,计算即得结论.
解答 解:(1)依题意,设等比数列{an}的公比为q,则q>1,
∵a3+2是a2,a4的等差中项,
∴2(a3+2)=a2+a4,
又∵a2+a3+a4=28,
∴2(a3+2)=28-a3,
解得:a3=8,
∴$\frac{8}{q}$+8+8q=28,整理得:2q2-5q+2=0,
解得:q=2或q=$\frac{1}{2}$(舍),
∴an=a3•qn-3=2n;
(2)由(1)可知bn=log2a2n=2n,
则Sn=2•$\frac{n(n+1)}{2}$=n2+n,
∴Sn>40+4n等价于n2+n>40+4n,
整理得:n2-3n-40>0,
解得:n>8或n<-5(舍),
于是满足条件的正整数n的最小值为9.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
2.双曲线$\frac{x^2}{a^2}-{y^2}=1$的离心率为$\sqrt{2}$,则正数a的值为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
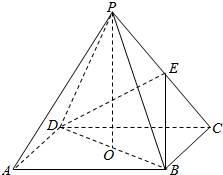 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.