题目内容
9.若 A,B是双曲线${x^2}-\frac{y^2}{3}=1$上两个动点,且$\overrightarrow{{O}{A}}•\overrightarrow{{O}{B}}=0$,则△AOB面积的最小值是$\frac{3}{2}$.分析 设直线OA的方程为y=kx,则直线OB的方程为y=-$\frac{1}{k}$x,设点A(x1,y1),y=kx与双曲线方程联立,可得x12=$\frac{3}{3-{k}^{2}}$,y12=$\frac{3{k}^{2}}{3-{k}^{2}}$,可求得|OA|2,|OB|2,|OA|2•|OB|2,利用基本不等式即可求得答案.
解答 解:设直线OA的方程为y=kx,则直线OB的方程为y=-$\frac{1}{k}$x,
设点A(x1,y1),y=kx与双曲线方程联立,可得x12=$\frac{3}{3-{k}^{2}}$,y12=$\frac{3{k}^{2}}{3-{k}^{2}}$,
∴|OA|2=x12+y12=$\frac{3+3{k}^{2}}{3-{k}^{2}}$,
同理|OB|2=$\frac{3+3{k}^{2}}{3{k}^{2}-1}$,
故|OA|2•|OB|2=$\frac{(3+3{k}^{2})^{2}}{-3+10{k}^{2}-3{k}^{4}}$
∵$\frac{{k}^{2}}{(1+{k}^{2})^{2}}$=$\frac{1}{{k}^{2}+\frac{1}{{k}^{2}}+2}$≤$\frac{1}{4}$(当且仅当k=±1时,取等号)
∴|OA|2•|OB|2≥9,又b>a>0,
故S△AOB=$\frac{1}{2}$|OA||OB|的最小值为$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查双曲线的简单性质与三角形的面积,考查基本不等式,考查转化与综合运算及抽象思维能力,属于难题.

练习册系列答案
相关题目
20.下面四个条件中,使a>b成立的必要而不充分的条件是( )
| A. | a+1>b | B. | 2a>2b | C. | a2>b2 | D. | lga>lgb |
18.从某学习小组的5名男生和4名女生中任意选取3名学生进行视力检测,其中至少要选到男生与女生各一名,则不同的选取种数有( )
| A. | 35 | B. | 70 | C. | 80 | D. | 140 |
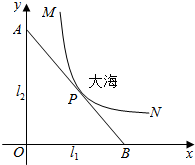 某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p. 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.