题目内容
已知a2+b2=1，x2+y2=1，求证ax+by≤1．
考点：不等式的证明
专题：不等式
分析：利用基本不等式的性质即可证明．
解答：
证明：∵a2+b2=1，x2+y2=1，
∴a2+b2+x2+y2=2，
∵a2+x2≥2ax，b2+y2≥2by，
∴2ax+2by≤2，
∴ax+by≤1
问题得以证明．
∴a2+b2+x2+y2=2，
∵a2+x2≥2ax，b2+y2≥2by，
∴2ax+2by≤2，
∴ax+by≤1
问题得以证明．
点评：本题主要考查基本不等式的性质，属于基础题．
练习册系列答案
天天向上口算本系列答案
相关题目
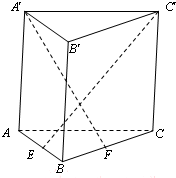如图，直三棱柱ABC-A′B′C′的侧棱长为3，AB⊥BC，且AB=BC=3，点E，F分别是棱AB，BC上的动点，且AE=BF，
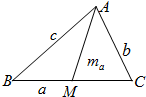如图：在△ABC中，角A，B，C的对边分别为a，b，c
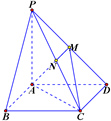如图，已知四棱锥P-ABCD的底面是边长为2的正方形，PA⊥底面ABCD，且PA=AD，点M、N分别为侧棱PD、PC的中点．
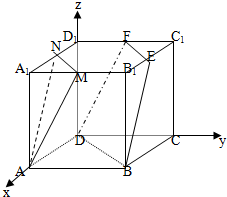如图，在正方体ABCD-A1B1C1D1中，M、N分别是棱A1B1、A1D1的中点，E、F分别是棱B1C1、C1D1的中点．求证：